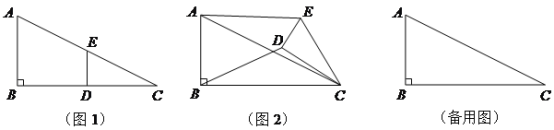
题目内容
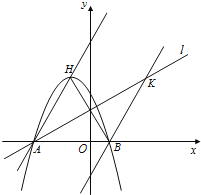
【题目】如图，抛物线y=mx
+2mx-3m(m≠0)的顶点为H，与
轴交于A、B两点（B点在A点右侧），点H、B关于直线l：
对称，过点B作直线BK∥AH交直线l于K点．
（1）求A、B两点坐标，并证明点A在直线I上。
（2）求此抛物线的解析式；
（3）将此抛物线向上平移，当抛物线经过K点时，设顶点为N，求出NK的长．
【答案】(1) A(-3,0) B(1,0) ； (2)y=-
x
-
x+
； (3)NK=4
【解析】
（1）令y=0，解关于x的一元二次方程，即可得到点A、B的坐标；然后把点A的坐标代入直线l的解析式，计算即可证明点A在直线上；
（2）根据轴对称的性质可得AH=AB，根据直线l的解析式求出直线l与x轴的夹角为30°，然后得到∠HAB的度数是60°，过点H作HC⊥x轴于点C，然后解直角三角形求出AC、HC，从而得到OC的长度，然后写出点H的坐标，再把点H的坐标代入抛物线解析式计算求出m的值，即可得解；
（3）根据平行直线的解析式的k值相等求出直线BK的解析式的k值，然后利用待定系数法求出直线BK的解析式，与直线l的解析式联立求解得到点K的值，再利用抛物线解析式求出相应横坐标上的点，从而求出抛物线向上移动的距离，然后得到平移后的抛物线的顶点N的坐标，根据两点间的距离公式计算即可得到NK的值．
令y=0，则mx2+2mx-3m=0（m≠0），
解得x1=-3，x2=1，
∵B点在A点右侧，
∴A点坐标为（-3，0），B点坐标为（1，0），
证明：∵直线l：
当x=-3时，
∴点A在直线l上；
（2）∵点H、B关于过A点的直线l：对称，
∴AH=AB=4，
设直线l与x轴的夹角为α，则
所以，∠α=30°，
∴∠HAB=60°，
过顶点H作HC⊥AB交AB于C点，
则
∴顶点H
代入抛物线解析式，得
解得m=-
所以，抛物线解析式为
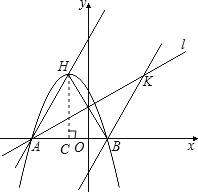
（3）∵BK∥AH
∴直线BK的k=tan60°=
设直线BK的解析式为y=x+b，
∵B点坐标为（1，0），
∴+b=0，
解得b=-，
∴直线BK的解析式为y=x-
联立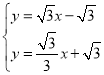
解得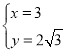
∴点K的坐标为（3，2 ），
当x=3时，
∴平移后与点K重合的点的坐标为（3，-6 ），
平移距离为2-（-6）=8，
∵平移前顶点坐标为（-1，2），
2+8=10，
∴平移后顶点坐标N（-1，10），
所以，NK的长是4
