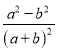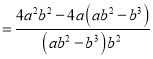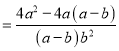ЬтФПФкШн
ЁОЬтФПЁПЁОЛиЙЫЁП
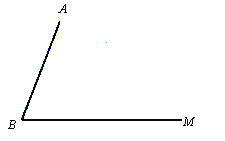
ШчЭМ1ЃЌЁїABCжаЃЌЁЯB=30ЁуЃЌAB=3ЃЌBC=4ЃЌдђЁїABCЕФУцЛ§ЕШгк ЃЎ
ЁОЬНОПЁП
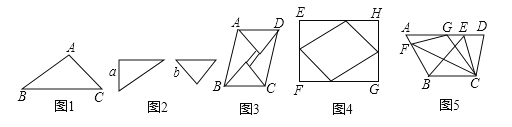
ЭМ2ЪЧЭЌбЇУЧЪьЯЄЕФвЛИБШ§НЧГпЃЌвЛИіКЌга30ЁуЕФНЧЃЌНЯЖЬЕФжБНЧБпГЄЮЊaЃЛСэвЛИіКЌга45ЁуЕФНЧЃЌжБНЧБпГЄЮЊbЃЌаЁУїгУСНИБетбљЕФШ§НЧГпЦДГЩвЛИіЦНааЫФБпаЮABCDЃЈШчЭМ3ЃЉЃЌгУСЫСНжжВЛЭЌЕФЗНЗЈМЦЫуЫќЕФУцЛ§ЃЌДгЖјЭЦГіsin75Ёу=![]() ЃЌаЁРігУСНИБетбљЕФШ§НЧГпЦДГЩСЫвЛИіОиаЮEFGHЃЈШчЭМ4ЃЉЃЌвВЭЦГіsin75Ёу=
ЃЌаЁРігУСНИБетбљЕФШ§НЧГпЦДГЩСЫвЛИіОиаЮEFGHЃЈШчЭМ4ЃЉЃЌвВЭЦГіsin75Ёу=![]() ЃЌЧыФуаДГіаЁУїЛђаЁРіЭЦГіsin75Ёу=
ЃЌЧыФуаДГіаЁУїЛђаЁРіЭЦГіsin75Ёу=![]() ЕФОпЬхЫЕРэЙ§ГЬЃЎ
ЕФОпЬхЫЕРэЙ§ГЬЃЎ
ЁОгІгУЁП
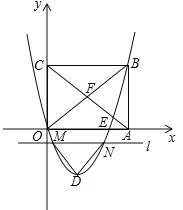
дкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯD=75ЁуЃЌBC=6ЃЌCD=5ЃЌAD=10ЃЈШчЭМ5ЃЉЃЎ
ЃЈ1ЃЉЕуEдкADЩЯЃЌЩшt=BE+CEЃЌЧѓt2ЕФзюаЁжЕЃЛ
ЃЈ2ЃЉЕуFдкABЩЯЃЌНЋЁїBCFбиCFЗелЃЌЕуBТфдкADЩЯЕФЕуGДІЃЌЕуGЪЧADЕФжаЕуТ№ЃПЫЕУїРэгЩЃЎ
ЁОД№АИЁПЁОЛиЙЫЁП3ЃЛЁОЬНОПЁПД№АИМћНтЮіЃЛЁОгІгУЁПЃЈ1ЃЉ86+25![]() ЃЛЃЈ2ЃЉЕуGВЛЪЧADЕФжаЕуЃЎ
ЃЛЃЈ2ЃЉЕуGВЛЪЧADЕФжаЕуЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЛиЙЫЃКШчЭМ1жаЃЌзїAHЁЭBCЃЎЧѓГіAHМДПЩНтОіЮЪЬтЃЛ
ЬНОПЃКШчЭМ2жаЃЌИљОнSЫФБпаЮABCD=BCABsin75Ёу=2SЁїABE+2SЁїBFC+SОиаЮEFGHСаГіЗНГЬМДПЩНтОіЮЪЬтЃЛ
гІгУЃКЃЈ1ЃЉзїCЙигкADЕФЖдГЦЕуHЃЌCHНЛADгкJЃЌСЌНгBHЃЌEHЃЎвђЮЊEC=EHЃЌЭЦГіEB+EC=EB+EHЃЌдкЁїEBHжаЃЌBE+EHЁнBHЃЌЭЦГіBE+ECЕФзюаЁжЕЮЊBHЃЌЧѓГіBHМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉНсТлЃКЕуGВЛЪЧADЕФжаЕуЃЎРэгЩЗДжЄЗЈжЄУїМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКгЩЬтвтПЩжЊЫФБпаЮEFGHЪЧОиаЮЃЌAB=CD=2aЃЌAH=DH=BF=CF=bЃЌEF=GH=![]() aЉbЃЌEH=FG=bЉaЃЌBC=
aЉbЃЌEH=FG=bЉaЃЌBC=![]() bЃЎ
bЃЎ
ЁОЛиЙЫЁПШчЭМ1жаЃЌзїAHЁЭBCЃЎ
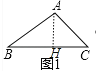
дкRtЁїABHжаЃЌЁпЁЯB=30ЁуЃЌAB=3ЃЌЁрAH=ABsin30Ёу=![]() ЃЌЁрSЁїABC=
ЃЌЁрSЁїABC=![]() BCAH=
BCAH=![]() ЁС4ЁС
ЁС4ЁС![]() =3ЃЌЙЪД№АИЮЊЃК3ЃЎ
=3ЃЌЙЪД№АИЮЊЃК3ЃЎ
ЬНОПЃКШчЭМ3жаЃЌ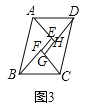
гЩЬтвтПЩжЊЫФБпаЮEFGHЪЧОиаЮЃЌAB=CD=2aЃЌAH=DH=BF=CF=bЃЌEF=GH=![]() aЉbЃЌEH=FG=bЉaЃЌBC=
aЉbЃЌEH=FG=bЉaЃЌBC=![]() bЃЌЁпSЫФБпаЮABCD=BCABsin75Ёу=2SЁїABE+2SЁїBFC+SОиаЮEFGH
bЃЌЁпSЫФБпаЮABCD=BCABsin75Ёу=2SЁїABE+2SЁїBFC+SОиаЮEFGH
Ёр![]() b2asin75Ёу=2ЁС
b2asin75Ёу=2ЁС![]() ЁСaЁС
ЁСaЁС![]() a+2ЁС
a+2ЁС![]() ЁСb2+ЃЈ
ЁСb2+ЃЈ![]() aЉbЃЉЃЈbЉaЃЉЃЌЁр2
aЉbЃЉЃЈbЉaЃЉЃЌЁр2![]() absin75Ёу=
absin75Ёу=![]() ab+abЃЌЁрsin75Ёу=
ab+abЃЌЁрsin75Ёу=![]() ЃЎ
ЃЎ
ШчЭМ4жаЃЌ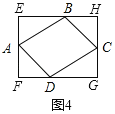
взжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЁЯBAD=75ЁуЃЌЁрSЫФБпаЮEFGH=2SЁїABE+2SЁїADF+SЦНааЫФБпаЮABCDЃЌЁрЃЈa+bЃЉЃЈ![]() a+bЃЉЈT2ЁС
a+bЃЉЈT2ЁС![]() ЁСaЁС
ЁСaЁС![]() a+2ЁС
a+2ЁС![]() ЁСb2+
ЁСb2+![]() b2asin75ЁуЃЌЁрsin75Ёу=
b2asin75ЁуЃЌЁрsin75Ёу=![]() ЃЎ
ЃЎ
гІгУЃКЃЈ1ЃЉзїCЙигкADЕФЖдГЦЕуHЃЌCHНЛADгкJЃЌСЌНгBHЃЌEHЃЎ
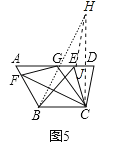
дкRtЁїDCJжаЃЌJC=CDsin75Ёу=![]() ЃЌЁрCH=2CJ=
ЃЌЁрCH=2CJ=![]() ЃЌдкRtЁїBHCжаЃЌBH2=BC2+CH2=36+
ЃЌдкRtЁїBHCжаЃЌBH2=BC2+CH2=36+![]() =86+25
=86+25![]() ЃЌЁпEC=EHЃЌЁрEB+EC=EB+EHЃЌдкЁїEBHжаЃЌBE+EHЁнBHЃЌЁрBE+ECЕФзюаЁжЕЮЊBHЃЌЁрt=BE+CEЃЌt2ЕФзюаЁжЕЮЊBH2ЃЌМДЮЊ86+25
ЃЌЁпEC=EHЃЌЁрEB+EC=EB+EHЃЌдкЁїEBHжаЃЌBE+EHЁнBHЃЌЁрBE+ECЕФзюаЁжЕЮЊBHЃЌЁрt=BE+CEЃЌt2ЕФзюаЁжЕЮЊBH2ЃЌМДЮЊ86+25![]() ЃЎ
ЃЎ
ЃЈ2ЃЉНсТлЃКЕуGВЛЪЧADЕФжаЕуЃЎ
РэгЩЃКзїCJЁЭADгкJЃЌDHЁЭCGгкHЃЎ
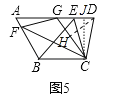
ВЛЗСЩшAG=GD=5ЃЌЁпCD=5ЃЌЁрDC=DGЃЌЁпDHЁЭCGЃЌЁрGH=CH=3ЃЌдкRtЁїCDHжаЃЌDH=![]() =
=![]() =4ЃЌЁпSЁїDGC=
=4ЃЌЁпSЁїDGC=![]() CGDH=
CGDH=![]() DGCJЃЌЁрCJ=
DGCJЃЌЁрCJ=![]() ЃЌЁрsinЁЯCDJ=
ЃЌЁрsinЁЯCDJ=![]() ЃЌЁпЁЯCDJ=75ЁуЃЌЁргыsin75Ёу=
ЃЌЁпЁЯCDJ=75ЁуЃЌЁргыsin75Ёу=![]() УЌЖмЃЌЁрМйЩшВЛГЩСЂЃЌЁрЕуGВЛЪЧADЕФжаЕуЃЎ
УЌЖмЃЌЁрМйЩшВЛГЩСЂЃЌЁрЕуGВЛЪЧADЕФжаЕуЃЎ