题目内容
【题目】如图，△OAB的一边OB在x轴的正半轴上，点A的坐标为（6，8），OA=OB，点P在线段OB上，点Q在y轴的正半轴上，OP=2OQ，过点Q作x轴的平行线分别交OA，AB于点E，F．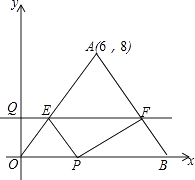
（1）求直线AB的解析式；
（2）若四边形POEF是平行四边形，求点P的坐标；
（3）是否存在点P，使△PEF为直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵A（6，8），∴OA= 
=10，
∴OB=OA=10，即B（10，0），
设直线AB解析式为y=kx+b，
把A与B坐标代入得： 
，
解得：k=﹣2，b=20．
则直线AB解析式为y=﹣2x+20
（2）
解：由A（6，8），得到直线OA解析式为y= 
x，
设OQ=t，则有OP=2OQ=2t，
把y=t代入y= x得：x= 
t；代入y=﹣2x+20得：x=10﹣ 
t，
∴E（ t，t），F（10﹣ t，t），
∴EF=10﹣ t﹣ t=10﹣ 
t，
若四边形POEF为平行四边形，则有EF=OP，即10﹣ t=2t，
解得：t= 
（3）
解：分三种情况考虑：
若∠PEF=90°，则有 t=2t，无解，不可能；
若∠PFE=90°，则有10﹣ 
=2t，解得：t=4，此时OP=8，即P（8，0）；
若∠EPF=90°，过E、F分别作x轴垂线，垂足分别为G、H，
∴Rt△EGP∽Rt△PHF，
∴ 
= 
，即 
= 
，
解得：t= 
，此时P= 
，即P（ ，0）．
综上，P的坐标为（8，0）或（ ，0）
【解析】（1）由A坐标确定出OA的长，即为OB的长，确定出B坐标，利用待定系数法求出直线AB解析式即可；（2）由A坐标确定出直线OA解析式，设OQ=t，则有OP=2t，表示出E与F坐标，进而表示出EF长，由四边形POEF为平行四边形，得到EF=OP，求出t的值，即可确定出P坐标；（3）分三种情况考虑：若∠PEF=90°；若∠PFE=90°；若∠EPF=90°，过E、F分别作x轴垂线，垂足分别为G、H，分别求出t的值，确定出满足题意P坐标即可．
【考点精析】认真审题，首先需要了解确定一次函数的表达式(确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法)，还要掌握平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)的相关知识才是答题的关键．
