题目内容
【题目】定义{a,b,c}为函数y=ax2+bx+c的“特征数”.
(1)“特征数”为{﹣1,2,3}的函数解析式为 , 将“特征数”为{0,1,1}的函数向下平移两个单位以后得到的函数解析式为;
(2)我们把横、纵坐标均为整数的点称为“整点”,试问:在上述两空填写的函数图象围成的封闭图形(包含边界)内共有多少个整点?请给出详细的运算过程;
(3)定义“特征数”的运算:①{a1 , b1 , c1}+{a2 , b2 , c2}={a1+a2 , b1+b2 , c1+c2};②λ{a1 , b1 , c1}={λa1 , λb1 , λc1}(其中λ为任意常数).试问:“特征数”为{﹣1,2,3}+λ{0,1,﹣1}的函数是否过定点?如果过定点,请计算出该定点坐标;如果不存在,请说明你的理由.
【答案】
(1)y=﹣x2+2x+3;y=x﹣1
(2)
解:
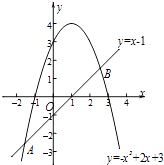
联立直线与二次函数方程 ![]()
解得: ![]() ,
,
估算﹣2<xA<﹣1,2<xB<3,
横坐标为﹣1的整点有:
(﹣1,0),(﹣1,﹣1),(﹣1,﹣2)三个;
横坐标为0的整点有:
(0,3),(0,2)(0,1),(0,0),(0,﹣1)五个;
横坐标为1的整点有:
(1,4),(1,3),(1,2),(1,1),(1,0)五个;
横坐标为2的整点有:
(2,3)(2,2)(2,1)三个;
合计,共16个整点
(3)
解:依据定义,{﹣1,2,3}+λ{0,1,﹣1}={﹣1,2+λ,3﹣λ},
∴该函数解析式为:y=﹣x2+(2+λ)x+3﹣λ=(﹣x2+2x+3)+λ(x﹣1),
令x﹣1=0,即x=1,解得:y=4,
∴该函数始终过定点(1,4).
【解析】解:(1)①根据定义,“特征数”为{﹣1,2,3},则可知a=﹣1,b=2,c=3,
则函数解析式为:y=﹣x2+2x+3,
②“特征数”为{0,1,1},则可知a=0,b=1,c=1,
∴y=x+1,
∴向下平移两个单位后得到的函数解析式为:y=x﹣1,
所以答案是:y=﹣x2+2x+3,y=x﹣1;
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.