题目内容

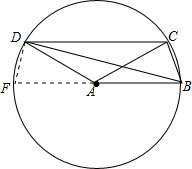
如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2．则BD的长为（　　）
A．
14
B．
15
C．3
2
D．2
3

以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．
∵DC∥AB，
∴
DF
=
BC
，
∴DF=CB=1，BF=2+2=4，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
BF2-DF2
=
15
．
故选B．
练习册系列答案
相关题目
刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①中，∠B=90°，∠A=30°，BC=6cm；图②中，∠D=90°，∠E=45°，DE=4cm．图③是刘卫同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上（移动开始时点D与点A重合）．
（1）在△DEF沿AC方向移动的过程中，刘卫同学发现：F、C两点间的距离逐渐______．（填“不变”、“变大”或“变小”）
（2）刘卫同学经过进一步地研究，编制了如下问题：
问题①：当△DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行？
问题②：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形？
问题③：在△DEF的移动过程中，是否存在某个位置，使得∠FCD=15°？如果存在，求出AD的长度；如果不存在，请说明理由．
请你分别完成上述三个问题的解答过程．
如图，EFGH是正方形ABCD的内接四边形，两条对角线EG和FH相交于点O，且它们所夹的锐角为θ，∠BEG与∠CFH都是锐角，已知EG=k，FH=l，四边形EFGH的面积为S，
（1）求证：sinθ=
2S
kl
；
（2）试用k、l、S来表示正方形ABCD的面积．
如图，长方形各边均与坐标轴平行或垂直，已知点A，C的坐标为A(
3
，-1)，C(-
3
，1)
（1）求B、D的坐标．
（2）将长方形ABCD先向左平移
3
个单位长度，再向下平移1个单位长度，所的四边形的四个顶点的坐标各是多少？
（3）求平移后的长方形的面积．
如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为7m，梯子的顶端B到地面的距离为24m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于15m．同时梯子的顶端B下降至B′，那么BB′等于（　　）
A．3mB．4mC．5mD．6m
△ABC中，AB=AC=13，若AB边上的高CD=5，则BC=______．
梯形ABCD中，AD∥BC，AB⊥BC，BC=DC，∠C=30°，AD=a，则BC的长为（　　）
A．（4+2
3
）a		B．（2+
3
）a		C．（4-2
3
）a		D．（2-
3
）a
在△ABC中，AB=15，AC=13，BC边上的高AD=12，则边BC的长是（　　）
A．14B．4C．14或4D．
56
如图将一根15cm长的细木棒放入长宽分别为4cm，3cm和12cm的长方体无盖盒子中，则细木棒露在外面的最短长度是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网