题目内容
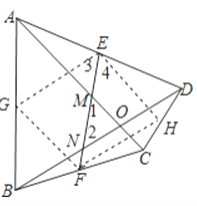
【题目】如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,EF分别交AC、BD于M、N,且OM=ON.
求证:AC=BD.

【答案】证明见解析
【解析】分析:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,根据中位线的性质得出OM=ON,从而得出∠4=∠EFH,即EH=HF,得出答案.
详解:证明:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,
则EH∥AC,EH=![]() AC,HF∥BD,FH=
AC,HF∥BD,FH=![]() BD,∴∠3=∠2,∠1=∠4,∵OM=ON,
BD,∴∠3=∠2,∠1=∠4,∵OM=ON,
∴∠1=∠2,∴∠4=∠3=∠1=∠2,同理∠EFH=∠GFE=∠1=∠2,∴∠4=∠EFH,
∴EH=HF,∵EH=![]() AC,FH=
AC,FH=![]() BD,∴AC=BD.
BD,∴AC=BD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目