题目内容
【题目】如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.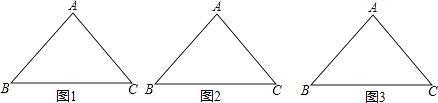
(1)小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).
(2)小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.
(3)若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”.
【答案】
(1)
解:作线段BC的中垂线AM,如图1所示.

∵AM是BC的中垂线,
∴BM=CM,
∴S△ABM=S△ACM,
∵AB=AC,
∴AB+BM=AC+CM.
∴直线AM是△ABC的等分积周线
(2)
解:小华不会成功.

若直线CD平分△ABC的面积,过点C作CE⊥AB于点E,如图2所示.
由S△ACD=S△BCD,得 ![]() ADCE=
ADCE= ![]() BDCE,于是BD=AD.
BDCE,于是BD=AD.
∵AC≠BC,
∴AD+AC≠BD+BC,
所以小华不会成功
(3)
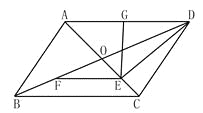
解:设直线EF与AB、BC分别交于点E、F,直线EF符合条件,如图3所示.

作EG⊥BC于点G,AH⊥BC于点H,得BH=CH=3,AH=4,S△ABC=12.
设BF=x,则BE= ![]() (AB+AC+BC)﹣BF=8﹣x.
(AB+AC+BC)﹣BF=8﹣x.
∵EG∥AH,
∴△BEG∽△BAH,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,于是EG=
,于是EG= ![]() (8﹣x)
(8﹣x)
∵S△EBF= ![]() S△ABC,
S△ABC,
∴ ![]() x
x ![]() (8﹣x)=6
(8﹣x)=6
解得 x=3(舍去,因此时EF过点A)或x=5
∴BF=5,BE=3.
∴直线EF符合条件
【解析】(1)作线段BC的中垂线即可.(2)小华不会成功.如图2所示.假设直线CD平分△ABC的面积,过点C作CE⊥AB于点E,再证明AD+AC≠BD+BC即可.(3)如图3所示,设直线EF与AB、BC分别交于点E、F,直线EF符合条件,作EG⊥BC于点G,AH⊥BC于点H,得BH=CH=3,AH=4,S△ABC=12,设BF=x,则BE= ![]() (AB+AC+BC)﹣BF=8﹣x,由△BEG∽△BAH,得
(AB+AC+BC)﹣BF=8﹣x,由△BEG∽△BAH,得 ![]() ,求出EG,利用面积列出方程即可解决问题.
,求出EG,利用面积列出方程即可解决问题.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】某车间一周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +5 | ﹣5 | +5 | +10 | ﹣10 | ﹣15 |
(1)本周三生产了多少辆电动车?
(2)本周总产量与计划总生产量相比,是增加多少辆?还是减少多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
(4)请你用折线图画出电动车产量的变化情况.