Question

【题目】在中，，为中点，点在线段上，连接，在下方有一点，满足，连接．

（1）若，，求的面积；

（2）若，，求证：．

Answer 1

【答案】（1）；（2）见解析．

【解析】

（1）先证明AB⊥AC，再求出∠B=30°，然后根据直角三角形斜边中线的性质可得出BC的长，再结合勾股定理可得出AB，AC的长，根据△ABE的面积=△ABC的面积可求出结果；

（2）延长CN至G，使CG=AC，易得△ACM≌△GCM，再证明∠NMC=∠MAE，在MC上截取MF=AE，可得出△MAE≌△NMF，结合已知再推出ME=CN=FN=CF，即△NCF为等边三角形，继而有∠MCN=60°，因此可得到∠ACB=60°，有AB=BC，结合AE=BC最终可得出结果．

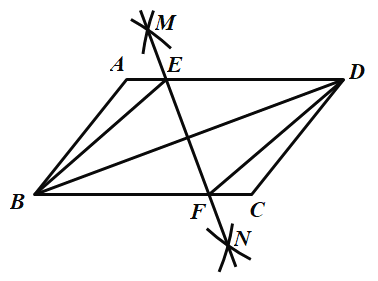
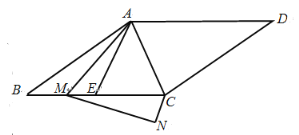
（1）解：∵四边形ABCD为平行四边形，

∴AB∥CD，AD∥BC，

∴∠CAD=∠ACB=∠BCN=60°，

又AC⊥CD，

∴AB⊥AC，∴∠B=30°，

在Rt△ABC中，E为BC的中点，

∴BC=2AE=10，

∴AC=BC=5，

∴AB=，

∴△ABE的面积=△ABC的面积=××AB×AC=．

（2）证明：延长CN至G，使CG=AC，

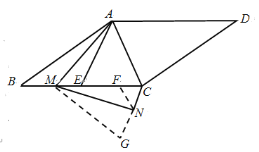
由（1）知∠ACM=∠GCM，

又MC=MC，

∴△ACM≌△GCM（SAS），

∴AM=GM，∠MAC=∠G，

又AM=MN，∴GM=MN，

∴∠G=∠MNG=∠MAC=∠MAE+∠EAC．

又由（1）易得，EC=EA，∴∠EAC=∠ACE=∠NCM，

∵∠MNG=∠NCM+∠NMC，

∴∠NMC=∠MAE，

在MC上截取MF=AE，

∴△MAE≌△NMF（SAS），

∴ME=FN，

又MC=ME+CE=MF+CF，MC=EA+CN，

∵EA=MF=CE，

∴ME=CN=CF=FN，

∴△NCF为等边三角形，

∴∠MCN=60°，

∴∠ACB=60°，

∴sin∠ACB==，

∴AB=BC，

又AE=BC，

∴．