题目内容
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).
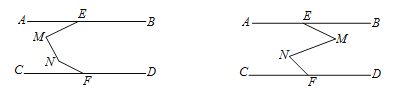
【答案】(1)∠EMF=∠AEM+∠MFC,∠AEM+∠EMF+∠MFC=360°(2)第一图数量关系:∠EMN+∠MNF-∠AEM-∠NFC=180°.第二图数量关系:∠EMN-∠MNF+∠AEM+∠NFC=180°.
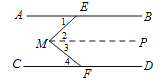
【解析】试题分析:(1)分点M在EF的左侧和右侧两种情况,当点M在EF的左侧时,如图,∠EMF=∠AEM+∠MFC,过点M作MP∥AB,可得AB∥CD∥MP, 根据平行线的性质可得∠4=∠3, ∠1=∠2,即可证得∠EMF=∠AEM+∠MFC;当点M在EF的右侧时,类比左侧的方法即可证得∠AEM+∠EMF+∠MFC=360°;(2)类比(1)的方法作平行线,利用平行线的性质即可解决.
试题解析:
(1)∠EMF=∠AEM+∠MFC.
证明:过点M作MP∥AB.
∵AB∥CD,
∴MP∥CD.
∴∠4=∠3.
∵MP∥AB,
∴∠1=∠2.
∵∠EMF=∠2+∠3,
∴∠EMF=∠1+∠4.
∴∠EMF=∠AEM+∠MFC.
∠AEM+∠EMF+∠MFC=360°
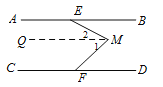
证明:过点M作MQ∥AB.
∵AB∥CD,
∴MQ∥CD.
∴∠CFM+∠1=180°.
∵MQ∥AB,
∴∠AEM+∠2=180°.
∴∠CFM+∠1+∠AEM+∠2=360°
∵∠EMF=∠1+∠2
∴∠AEM+∠EMF+∠MFC=360°.
(2)第一图数量关系:∠EMN+∠MNF-∠AEM-∠NFC=180°.
第二图数量关系:∠EMN-∠MNF+∠AEM+∠NFC=180°.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案