题目内容
【题目】如图,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线y=3x-4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=![]() 也经过A点.
也经过A点.
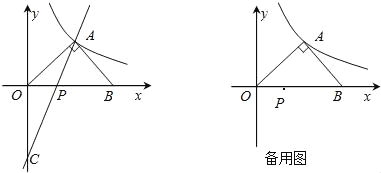
(1)求点A的坐标和k的值;
(2)若点P为x轴上一动点.在双曲线上是否存在一点Q,使得△PAQ是以点A为直角顶点的等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标为(2,2),k=4;(2) 在双曲线上存在一点Q(4,1),使得△PAQ是以点A为直角顶点的等腰三角形.
【解析】
试题分析:(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,根据直角三角形的性质可设点A的坐标为(a,a),因为点A在直线y=3x-4上,即把A点坐标代入解析式即可算出a的值,进而得到A点坐标,然后再利用待定系数法求出反比例函数解析式;
(2)如果过B作BQ⊥x轴交双曲线于Q点,连接AQ,过A点作AP⊥AQ交x轴于P点.由ASA易证△AOP≌△ABQ,得出AP=AQ,那么△APQ是所求的等腰直角三角形.根据全等三角形的性质及函数图象与点的坐标的关系得出结果.
试题解析:(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,
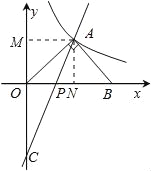
∵△AOB是等腰直角三角形,
∴AM=AN.
设点A的坐标为(a,a),
∵点A在直线y=3x-4上,
∴a=3a-4,
解得a=2,
则点A的坐标为(2,2),
∵双曲线y=![]() 也经过A点,
也经过A点,
∴k=4;
(2)假设双曲线上存在一点Q,使得△PAQ是等腰直角三角形.
过B作BQ⊥x轴交双曲线于Q点,连接AQ,过A点作AP⊥AQ交x轴于P点,
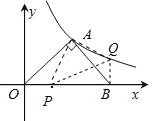
则△APQ为所求作的等腰直角三角形.
理由:在△AOP与△ABQ中,
∵∠OAB-∠PAB=∠PAQ-∠PAB,
∴∠OAP=∠BAQ,
在△AOP和△ABQ中
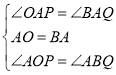 ,
,
∴△AOP≌△ABQ(ASA),
∴AP=AQ,
∴△APQ是所求的等腰直角三角形.
∵B(4,0),
∴Q(4,1),
经检验,在双曲线上存在一点Q(4,1),使得△PAQ是以点A为直角顶点的等腰三角形.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案