题目内容
【题目】△ABC为等边三角形，边长为a，DF⊥AB．EF⊥AC
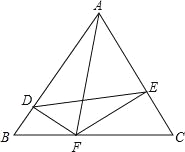
（1）求证：△BDF∽△CEF；
（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系式，并探究当m为何值时S取最大值．
【答案】（1）证明见解析；（2）最大值为3
．
【解析】
试题分析：（1）由等边三角形的性质得出∠B=∠C=60°，由已知得出∠BDF=∠CEF=90°，即可证出△BDF∽△CEF；
（2）作AM⊥BC于M，由等边三角形的性质得出AB=BC=4，BM=CM=
BC=2，由勾股定理求出AM，得出△ABC的面积；求出∠DFB=∠EFC=30°，由含30°角的直角三角形的性质得出BD=BF=m，CE=CF=（4-m），得出DF、EF的长度，求出△BDF和△CEF的面积，由四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积，得出S与m之间的函数关系式为S=-
m2+m+2；化成顶点式，得出当m=2时，S取最大值为3即可．
试题解析：（1）∵△ABC为等边三角形，
∴∠B=∠C=60°，
∵DF⊥AB．EF⊥AC，
∴∠BDF=∠CEF=90°，
∴△BDF∽△CEF；
（2）作AM⊥BC于M，如图所示：
∵△ABC是等边三角形，
∴AB=BC=4，BM=CM=BC=2，
∴AM=
=
=2，
∴△ABC的面积=BCAM=×4×2=4，
∵BF=m，
∴CF=4-m，
∵∠BDF=∠CEF=90°，∠B=∠C=60°，
∴∠DFB=∠EFC=30°，
∴BD=BF=m，CE=CF=（4-m），
∴DF=BD=
m，EF=CE=（4-m），
∴△BDF的面积=BDDF=×m×m=
m2，
△CEF的面积=CEEF=×（4-m）×（4-m）=（4-m）2，
∴四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积=4-m2-（4-m）2=-m2+m+2，
即S与m之间的函数关系式为S=-m2+m+2；
又∵S=-m2+m+2=-（m-2）2+3，-＜0，
∴当m=2时，S取最大值为3．
