题目内容
某工厂设计了一款产品,成本价为每件20元.投放市场进行试销,得到如下数据:
(I)若日销售量 (件)是售价
(件)是售价 (元∕件)的一次函数,求这个一次函数解析式;
(元∕件)的一次函数,求这个一次函数解析式;
(II)设这个工厂试销该产品每天获得的利润(利润=销售价-成本价)为W(元),当售价定为每件多少元时,工厂每天获得的利润最大?最大利润是多少元?
售价 (元∕件) (元∕件) | …… | 30 | 40 | 50 | 60 | …… |
日销售量 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |
 (件)是售价
(件)是售价 (元∕件)的一次函数,求这个一次函数解析式;
(元∕件)的一次函数,求这个一次函数解析式;(II)设这个工厂试销该产品每天获得的利润(利润=销售价-成本价)为W(元),当售价定为每件多少元时,工厂每天获得的利润最大?最大利润是多少元?
(I)设这个一次函数解析式为 y=kx+b(k≠0).
∴
解得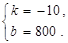
∴y=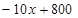 .
.
(II)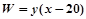
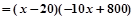 分
分
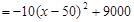 .
.
∴当售价定为50元时,工艺厂每天获得的利润W最大,最大利润是9000元.
∴

解得
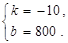
∴y=
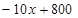 .
. (II)
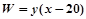
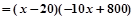 分
分 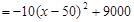 .
. ∴当售价定为50元时,工艺厂每天获得的利润W最大,最大利润是9000元.
(1)由图可猜想y与x是一次函数关系,任选两点求表达式即可,
(2)利润=销售总价-成本总价=单件利润×销售量.据此得表达式,运用性质求最值;
(2)利润=销售总价-成本总价=单件利润×销售量.据此得表达式,运用性质求最值;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
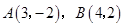 两点,现另取一点
两点,现另取一点 ,当
,当 时,
时, 的值最小.
的值最小.
 的图像经过点(2,3),则
的图像经过点(2,3),则 的值为 ▲
的值为 ▲ 
 台,所有型号空调全部售出后获得的总利润为
台,所有型号空调全部售出后获得的总利润为 元.
元. 元(
元( ),其余型号售价不变,则商场又该如何采购才能获得最大利润?
),其余型号售价不变,则商场又该如何采购才能获得最大利润?
 和
和 的位置可能为:
的位置可能为:



