题目内容
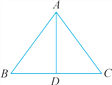
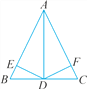
【题目】如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:DE=DF.
(2)问:如果DE,DF分别是∠ADB,∠ADC的平分线,那么它们还相等吗?
【答案】(1)见解析;(2)相等,理由见解析
【解析】试题分析:(1)D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF.
(2)由(1)知,∠DAE=∠DAF,∠ADB=∠ADC=90°,由角平分线定义知∠ADE=∠ADF,再由ASA证明△ADE与△ADF全等,即可得证.
试题解析:(1)∵D是BC的中点,AB=AC,
∴AD是等腰三角形ABC的角平分线,
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)相等.理由如下:
由(1)知AD⊥BC,∠DAE=∠DAF,
∴∠ADB=∠ADC=90°.
∵DE,DF分别是∠ADB,∠ADC的平分线,
∴∠ADE=![]() ∠ADB,∠ADF=
∠ADB,∠ADF=![]() ∠ADC,
∠ADC,
∴∠ADE=∠ADF.
在△ADE和△ADF中,  ,
,
∴△ADE≌△ADF(ASA).
∴DE=DF.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目