题目内容
【题目】已知一次函数y=kx-6，当x=1时，y=2。求：
（1）k的值；
(2)当0≤x≤3时，求y的取值范围。
【答案】（1）k=8；(2)-6《y《18.
【解析】试题分析：（1）把x=1，y=2代入y=kx-6，即可求得k的值；
（2）先根据一次函数的性质判断出函数的增减性，再求出y最大值和最小值即可解答．
试题解析：（1）x=1，y=2代入y=kx-6中，
得： 2=k-6，
解得k=8；
（2）∵一次函数y=8x-6中k=8>0，
∴一次函数y=8x-6是增函数，
∴当x最小时，y最小，x最大时，y最大，
∵0≤x≤3，
∴当x=0时，y最小=-6；x=3时，y最大=18．
故答案为：-6<y<18.
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
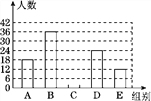
【题目】随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业个人旅游年消费情况进行问卷调查，随机抽查部分员工，记录每个人年消费金额，并将调查数据适当整理，绘制成尚不完整的表和图(如图)．
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000＜x≤4 000 | a | b |
C | 4 000＜x≤6 000 | ||
D | 6 000＜x≤8 000 | 24 | 0.20 |
E | x＞8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题：
(1)a＝________，b＝________，c＝________，并将条形统计图补充完整；
(2)在这次调查中，个人年消费金额的中位数出现在________组；
(3)若这个企业有3 000名员工，请你估计个人旅游年消费金额在6 000元以上的人数．
