题目内容
【题目】如图,△ABC中,AE=BE,∠AED =∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB = CB,∠AED =4∠EAD,求∠C的度数.
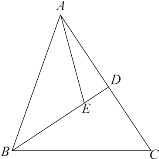
【答案】(1)见解析(2)54°
【解析】
(1)先根据AE=BE得到∠ABE=∠BAE,再由∠AED=∠ABC得到∠BAE=∠CBD,即可得到∠ABE=∠CBD,故可求解;
(2)先求出![]() ,再求出∠BAE=
,再求出∠BAE=![]() ,从而求出∠BAD,再根据AB=CB求∠C.
,从而求出∠BAD,再根据AB=CB求∠C.
(1)证明:∵AE=BE
∠ABE=∠BAE
∵∠AED=∠ABC 而∠AED=∠ABE+∠BAE,∠ABC=∠ABE+∠CBD
∴∠BAE=∠CBD
∴∠ABE=∠CBD,即 BD 平分∠ABC.
(2)解:若 AB=CB,由(1)知 BD 平分∠ABC
∴BD⊥AC
∴∠EDA=90°
∴∠AED+∠EAD=90°
∵∠AED=4∠EAD
∴![]()
∴∠BAE=![]()
∴∠BAD=36°+18°=54°
又∵AB=CB
∴∠C=∠BAD=54°

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目