Question

【题目】已知:CP是等边△ABC的外角∠ACE的平分线，点D在边BC上，以D为顶点，DA为一条边作∠ADF=60°,另一边交射线CP于F

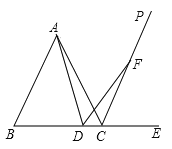
(1)求证:AD=FD

(2)若AB=2,BD=x,DF=y,求y关于x的函数解析式

(3)若点D在线段BC的延长线上，（1）中的结论还一定成立吗？若成立，请证明．

Answer 1

【答案】（1）见解析；（2）；（3）成立，证明见解析.

【解析】

（1）利用外角平分线得：∠ACP=∠PCE=60°，证明A、D、C、F四点共圆，从而得出△ADF是等边三角形，所以AD=FD；

（2）作AM⊥BC于M．证明AD2=AEAB，即可解决问题；

（3）同（1）得：A、C、D、F四点共圆，则△ADF 是等边三角形，所以AD=FD．

（1）连接AF，

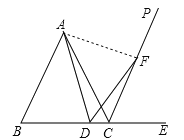
∵∠ACB=60°，

∴∠ACE=120°，

∵CP平分∠ACE，

∴∠ACP=∠PCE=60°，

∴∠ADF=∠ACP=60°，

∴A、D、C、F四点共圆，

∴∠AFD=∠ACB=60°，

∴∠ADF=∠AFD=60°，

∴∠DAF=60°，

∴△ADF是等边三角形，

∴AD=FD；

（2）过A作AM⊥BC于M，如图，

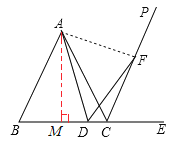
∵△ABC是等边三角形，

∴BC=AB=2，BM=BC=1，

∴AM=

∵BD=x，

∴MD=x-1，

∵△ADF是等边三角形，

∴AD=DF=y，

在Rt△AMD中，

∴，即；

（3）如图，

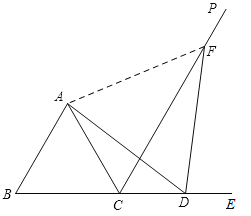
同（1）得：∠ADF=∠ACF=60°，

∴A、C、D、F四点共圆，

∴∠FAD=∠FCD=60°，

∴∠AFD=60°，

∴△ADF 是等边三角形，

∴AD=FD．