ЬтФПФкШн
ЁОЬтФПЁПФГЙЋЫОЩњВњЕФвЛжжНЁЩэВњЦЗдкЪаГЁЩЯЪмЕНЦеБщЛЖгЃЌУПФъПЩдкЙњФкЁЂЙњЭтЪаГЁЩЯШЋВПЪлЭъЃЌИУЙЋЫОЕФФъВњСПЮЊ6ЧЇМўЃЌШєдкЙњФкЪаГЁЯњЪлЃЌЦНОљУПМўВњЦЗЕФРћШѓ![]() ЃЈдЊЃЉгыЙњФкЯњЪлЪ§СП
ЃЈдЊЃЉгыЙњФкЯњЪлЪ§СП![]() ЃЈЧЇМўЃЉЕФЙиЯЕЮЊЃК
ЃЈЧЇМўЃЉЕФЙиЯЕЮЊЃК ШєдкЙњЭтЯњЪлЃЌЦНОљУПМўВњЦЗЕФРћШѓ
ШєдкЙњЭтЯњЪлЃЌЦНОљУПМўВњЦЗЕФРћШѓ![]() ЃЈдЊЃЉгыЙњЭтЕФЯњЪлЪ§СПtЃЈЧЇМўЃЉЕФЙиЯЕЮЊЃК
ЃЈдЊЃЉгыЙњЭтЕФЯњЪлЪ§СПtЃЈЧЇМўЃЉЕФЙиЯЕЮЊЃК
ЃЈ1ЃЉгУ![]() ЕФДњЪ§ЪНБэЪОtЮЊЃКt= ЃЛЕБ0ЃМ
ЕФДњЪ§ЪНБэЪОtЮЊЃКt= ЃЛЕБ0ЃМ![]() Ём4ЪБЃЌ
Ём4ЪБЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЮЊЃК
ЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() = ЃЛЕБ4Ём
= ЃЛЕБ4Ём![]() ЃМ ЪБЃЌ
ЃМ ЪБЃЌ![]() =100ЃЛ
=100ЃЛ
ЃЈ2ЃЉЧѓУПФъИУЙЋЫОЯњЪлетжжНЁЩэВњЦЗЕФзмРћШѓWЃЈЧЇдЊЃЉгыЙњФкЕФЯњЪлЪ§СПЃјЃЈЧЇМўЃЉЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіЃјЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉИУЙЋЫОУПФъЙњФкЁЂЙњЭтЕФЯњСПИїЮЊЖрЩйЪБЃЌПЩЪЙЙЋЫОУПФъЕФзмРћШѓзюДѓЃПзюДѓжЕЮЊЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ6ЃxЃЛ5xЃЋ80ЃЛ6ЃЈ2ЃЉ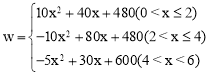 ЃЈ3ЃЉИУЙЋЫОУПФъЙњФкЁЂЙњЭтЕФЯњЪлСПИїЮЊ4ЧЇМўЁЂ2ЧЇМўЃЌПЩЪЙЙЋЫОУПФъЕФзмРћШѓзюДѓЃЌзюДѓжЕЮЊ64ЭђдЊ
ЃЈ3ЃЉИУЙЋЫОУПФъЙњФкЁЂЙњЭтЕФЯњЪлСПИїЮЊ4ЧЇМўЁЂ2ЧЇМўЃЌПЩЪЙЙЋЫОУПФъЕФзмРћШѓзюДѓЃЌзюДѓжЕЮЊ64ЭђдЊ
ЁОНтЮіЁПНтЃКЃЈ1ЃЉ6ЃxЃЛ5xЃЋ80ЃЛ6ЁЃ
ЃЈ2ЃЉЗжШ§жжЧщПіЃК
ЂйЕБ0ЃМxЁм2ЪБЃЌ![]() ЃЛ
ЃЛ
ЂкЕБ2ЃМxЁм4ЪБЃЌ![]() ЃЛ
ЃЛ
ЂлЕБ4ЃМxЃМ6ЪБЃЌ![]() ЁЃ
ЁЃ
злЩЯЫљЪіЃЌ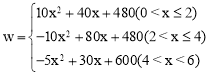 ЁЃ
ЁЃ
ЃЈ3ЃЉЕБ0ЃМxЁм2ЪБЃЌ![]() ЃЌДЫЪБx=2ЪБЃЌwзюДѓ=600ЃЛ
ЃЌДЫЪБx=2ЪБЃЌwзюДѓ=600ЃЛ
ЕБ2ЃМxЁм4ЪБЃЌ![]() ЃЌДЫЪБx=4ЪБЃЌwзюДѓ=640ЃЛ
ЃЌДЫЪБx=4ЪБЃЌwзюДѓ=640ЃЛ
ЕБ4ЃМxЃМ6ЪБЃЌ![]() ЃЌЁр4ЃМxЃМ6ЪБЃЌwЃМ640ЁЃЁЃ
ЃЌЁр4ЃМxЃМ6ЪБЃЌwЃМ640ЁЃЁЃ
злЩЯЫљЪіЃЌx=4ЪБЃЌwзюДѓ=640ЁЃ
ЙЪИУЙЋЫОУПФъЙњФкЁЂЙњЭтЕФЯњЪлСПИїЮЊ4ЧЇМўЁЂ2ЧЇМўЃЌПЩЪЙЙЋЫОУПФъЕФзмРћШѓзюДѓЃЌзюДѓжЕЮЊ64ЭђдЊЁЃ
ЃЈ1ЃЉгЩИУЙЋЫОЕФФъВњСПЮЊ6ЧЇМўЃЌУПФъПЩдкЙњФкЁЂЙњЭтЪаГЁЩЯШЋВПЪлЭъЃЌПЩЕУЙњФкЯњЪлСП+ЙњЭтЯњЪлСП=6ЧЇМўЃЌМДx+t=6ЃЌБфаЮМДЮЊt=6ЃxЃЛ
ИљОнЦНОљУПМўВњЦЗЕФРћШѓy2ЃЈдЊЃЉгыЙњЭтЕФЯњЪлЪ§СПtЃЈЧЇМўЃЉЕФЙиЯЕ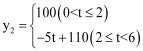 вдМА
вдМА
t=6ЃxМДПЩЧѓГіy2гыxЕФКЏЪ§ЙиЯЕЃКЕБ0ЃМxЁм4ЪБЃЌy2=5x+80ЃЛ
ЕБy2=100ЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЁЃ
ЁЃ
ЃЈ2ЃЉИљОнзмРћШѓ=ЙњФкЯњЪлЕФРћШѓ+ЙњЭтЯњЪлЕФРћШѓЃЌНсКЯКЏЪ§НтЮіЪНЃЌЗжШ§жжЧщПіЬжТлЃКЂй0ЃМxЁм2ЃЛЂк2ЃМxЁм4ЃЛЂл4ЃМxЃМ6ЁЃ
ЃЈ3ЃЉЯШРћгУХфЗНЗЈНЋИїНтЮіЪНаДГЩЖЅЕуЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪЃЌЧѓГіШ§жжЧщПіЯТЕФзюДѓжЕЃЌдйБШНЯМДПЩЁЃ

 НђЧХНЬг§МЦЫуаЁзДдЊЯЕСаД№АИ
НђЧХНЬг§МЦЫуаЁзДдЊЯЕСаД№АИ