Question

【题目】如图，∴P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长BP交边AD于点F，交CD的延长线于点G．

（1）求证：△APB≌△APD；

（2）已知DF：FA＝1：2，设线段DP的长为x，线段PF的长为y．

①求y与x的函数关系式；

②当x＝6时，求线段FG的长．

Answer 1

【答案】解：（1）证明：∵四边形ABCD是菱形，∴AB=AD，AC平分∠DAB。∠DAP=∠BAP。

∵在△APB和△APD中，，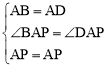

∴△APB≌△APD（SAS）。

（2）①∵四边形ABCD是菱形，∴AD∥BC，AD=BC。

∴△AFP∽△CBP。∴。

∵DF：FA＝1：2，∴AF：BC＝3：3。∴。

由（1）知，PB=PD=x，又∵PF=y，∴。

∴，即ｙ与x的函数关系式为。

②当x＝6时，，∴。

∵DG∥AB，∴△DFG∽△AFB。∴。∴。

∴，即线段FG的长为5。

【解析】

试题（1）由菱形的性质得到AB=AD，∠DAP=∠BAP，加上公共边AP=AP，根据SAS即可证得结论。

（2）①由△AFP∽△CBP列比例式即可得到ｙ与x的函数关系式。

②由函数关系式求得PF的长，从而得到FB的长，由△DFG∽△AFB列比例式即可得到线段FG的长。