题目内容
【题目】如图,在⊙O中,AB为直径,点M为AB延长线上的一点,MC与⊙O相切于点C,圆周上有另一点D与点C分居直径AB两侧,且使得MC=MD=AC,连接AD.现有下列结论:①MD与⊙O相切;②四边形ACMD是菱形;③AB=MO;④∠ADM=120°,其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】
如图,连接CO,DO,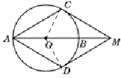
∵MC与⊙O相切于点C,
∴∠MCO=90°,
在△MCO与△MDO中,
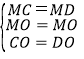 ,
,
∴△MCO≌△MDO(SSS),
∴∠MCO=∠MDO=90°,∠CMO=∠DMO,
∴MD与⊙O相切,故①正确;
在△ACM与△ADM中,
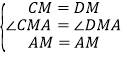 ,
,
∴△ACM≌△ADM(SAS),
∴AC=AD,
∴MC=MD=AC=AD,
∴四边形ACMD是菱形,故②正确;
如图连接BC,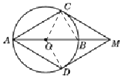
∵AC=MC,
∴∠CAB=∠CMO,
又∵AB为⊙O的直径,
∴∠ACB=90°,
在△ACB与△MCO中,
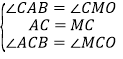 ,
,
∴△ACB≌△MCO(SAS),
∴AB=MO,故③正确;
∵△ACB≌△MCO,
∴BC=OC,
∴BC=OC=OB,
∴∠COB=60°,
∵∠MCO=90°,
∴∠CMO=30°,
又∵四边形ACMD是菱形,
∴∠CMD=60°,
∴∠ADM=120°,故④正确;
故正确的有4个.
故选A.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目





