题目内容
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
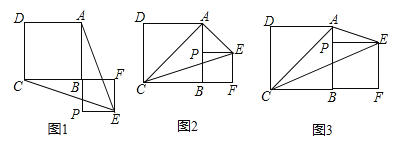
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
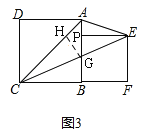
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
【答案】(1)证明见解析;(2)△ACE是直角三角形;(3)![]() :1,45°.
:1,45°.
【解析】
试题分析:(1)由正方形的性质证明△APE≌△CFE,可得结论;
(2)分别证明∠PAE=45°和∠BAC=45°,则∠CAE=90°,即△ACE是直角三角形;
(3)分别计算PG和BG的长,利用平行线分线段成比例定理列比例式得:![]() ,即
,即![]() ,解得:a=
,解得:a=![]() b,得出a与b的比,再计算GH和BG的长,由角平分线的逆定理得:∠HCG=∠BCG,由平行线的内错角得:∠AEC=∠ACB=45°.
b,得出a与b的比,再计算GH和BG的长,由角平分线的逆定理得:∠HCG=∠BCG,由平行线的内错角得:∠AEC=∠ACB=45°.
试题解析:(1)∵四边形ABCD和四边形BPEF是正方形,∴AB=BC,BP=BF,∴AP=CF,在△APE和△CFE中,∵AP=CF,∠P=∠F,PE=EF,∴△APE≌△CFE,∴EA=EC;
(2)△ACE是直角三角形,理由是:
如图2,∵P为AB的中点,∴PA=PB,∵PB=PE,∴PA=PE,∴∠PAE=45°,又∵∠BAC=45°,∴∠CAE=90°,即△ACE是直角三角形;
(3)设CE交AB于G,∵EP平分∠AEC,EP⊥AG,∴AP=PG=a﹣b,BG=a﹣(2a﹣2b)=2b﹣a,∵PE∥CF,∴![]() ,即
,即![]() ,解得:a=
,解得:a=![]() b,∴a:b=
b,∴a:b=![]() :1,作GH⊥AC于H,∵∠CAB=45°,∴HG=
:1,作GH⊥AC于H,∵∠CAB=45°,∴HG=![]() AG=
AG=![]() (2
(2![]() b﹣2b)=(2﹣
b﹣2b)=(2﹣![]() )b,又∵BG=2b﹣a=(2﹣
)b,又∵BG=2b﹣a=(2﹣![]() )b,∴GH=GB,GH⊥AC,GB⊥BC,∴∠HCG=∠BCG,∵PE∥CF,∴∠PEG=∠BCG,∴∠AEC=∠ACB=45°.
)b,∴GH=GB,GH⊥AC,GB⊥BC,∴∠HCG=∠BCG,∵PE∥CF,∴∠PEG=∠BCG,∴∠AEC=∠ACB=45°.

【题目】在东西向的马路上有一个巡岗亭![]() ,巡岗员从岗亭
,巡岗员从岗亭![]() 出发以
出发以![]() 速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
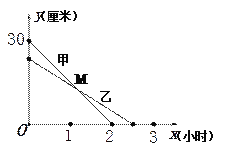
(1)第几次结束时巡逻员甲距离岗亭![]() 最远?距离
最远?距离![]() 有多远?
有多远?
(2)甲巡逻过程中配置无线对讲机,并一直与留守在岗亭![]() 的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?