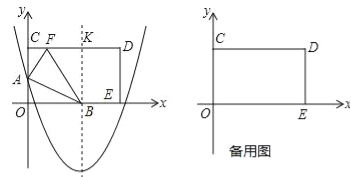
题目内容
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC= ![]() =
= ![]() =5,
=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
【解析】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
【考点精析】掌握角平分线的性质定理和勾股定理的概念是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】我市某中学今年年初开学后打算招聘一名数学老师,对三名前来应聘的数学老师A、B、C进行了考核,他们的笔试成绩和说课成绩(单位:分)分别用了两种方式进行了统计,如表和图1,
A | B | C | |
笔试 | 85 | 95 | 90 |
说课 | 80 | 85 |
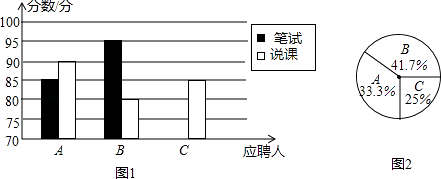
(1)请将表和图1的空缺部分补充完整;
(2)应聘的最后一个程序是由该校的24名数学教师进行投票,三位应聘者的得票情况如图2(没有弃权票,该校的每位教师只能选一位应聘教师),请计算每人的得票数(得票数可是整数哟)
(3)若每票计1分,该校将笔试、说课、得票三项测试得分按3:4:3的比例 确定个人成绩,请计算三位应聘者的最后成绩,并根据成绩判断谁能应聘成功.