Question

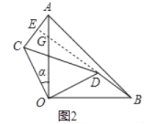
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置，直角顶点重合在点O处，AB=25，CD=17．保持纸片AOB不动，将纸片COD绕点O逆时针旋转α（0°<α<90°）角度，如图2所示．

（1）利用图2证明AC=BD且AC⊥BD；

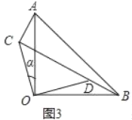
（2）当BD与CD在同一直线上（如图3）时，求AC的长和α的正弦值．

Answer 1

【答案】(1)证明见解析；（2）AC=7,

【解析】试题分析：（1）图形经过旋转以后，明确没有变化的边长，根据全等三角形的判定定理证明图中的△COA≌△DOB，从而证明AC=BD，做辅助△ABE，证明∠AEB=90°，从而得到AC⊥BD；

（2）在△COA中，根据余弦定理，得出cosα的值，从而求出sinα的值.

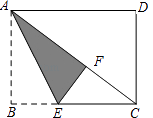
试题解析：（1）如图2中，延长BD交OA于G，交AC于E．

∵∠AOB=∠COD=90°，

∴∠AOC=∠DOB，

在△AOC和△BOD中， ，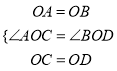

∴△AOC≌△BOD，

∴AC=BD，∠CAO=∠DBO，

∵∠DBO+∠GOB=90°，

∵∠OGB=∠AGE，

∴∠CAO+∠AGE=90°，

∴∠AEG=90°，

∴BD⊥AC．

（2）如图3中，设AC=x，

∵BD、CD在同一直线上，BD⊥AC，

∴△ABC是直角三角形，

∴AC2+BC2=AB2，

∴x2+（x+17）2=252，

解得x=7，

∵∠ODC=∠α+∠DBO=45°,∠ABC+∠DBO=45°,

∴∠α=∠ABC，

∴sinα=sin∠ABC==．