题目内容
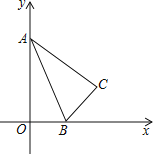
【题目】在平面直角坐标系中，点A（0，b）、点B（a，0）、点D（d，0）且a、b、c满足
．DE⊥x轴且∠BED=∠ABD，BE交y轴于点C，AE交x轴于点F．
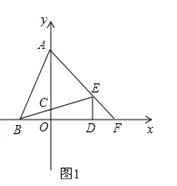
（1）求点A、B、D的坐标；
（2）求点C、E、F的坐标；
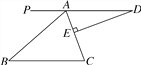
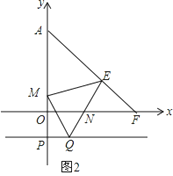
（3）如图，过P（0，-1）作x轴的平行线，在该平行线上有一点Q（点Q在P的右侧）使∠QEM=45°，QE交x轴于N，ME交y轴正半轴于M，求
的值．
【答案】(1)A(0,3) B(-1,0) D(2,0)；(2)
E(2,1) F(3,0)；(3)
【解析】
（1）由非负数的性质可求得a、b、d的值，可求得A、B、D的坐标；
（2）由条件可证明△ABO≌△BED，可求得DE和BD的长，可求得E点坐标，再求得直线AE与BE的解析式，可求得C、F点坐标；
（3）过E作EG⊥OA于点G，EH⊥PQ于点Q，可证明四边形GEHP为正方形，在GA上截GI=QH，可证明△IGE≌△QHE，可证得∠IEM=∠MEQ=45°，可证明△EIM≌△EQM，可得到IM=MQ，再结合条件可求得PH=AI=PQ，可求得答案．
解：（1）∵
，
∴
∴
，
∴A（0，3），B（-1，0），D（2，0）；
（2）∵A（0，3），B（-1，0），D（2，0），
∴OB=1，OD=2，OA=3，
∴AO=BD，
在△ABO和△BED中，
，
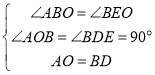∴△ABO≌△BED（AAS），
∴DE=BO=1，
∴E（2，1），
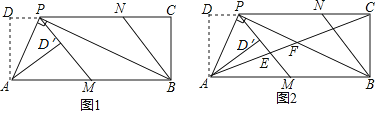
设直线AE解析式为：y=kx+b，直线BE解析式为：y=mx+n，如图1，
把点A、E代入y=kx+b，把点B、E代入y=mx+n，得
，
，
解得：
，
，
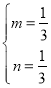∴直线AE解析式为：
，
直线BE解析式为：
，
∴直线，令
，解得：
，
∴点F为：
，
∴直线，令
，解得：
，
∴点C为：
；
（3）过E作EG⊥OA，EH⊥PQ，垂足分别为G、H，在GA上截取GI=QH，如图2，
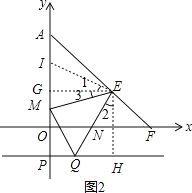
∵E（2，1），P（-1，0），
∴GE=GP=GE=PH=2，
∴四边形GEHP为正方形，
∴∠IGE=∠EHQ=90°，
在Rt△IGE和Rt△QHE中
，
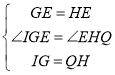∴△IGE≌△QHE（SAS），
∴IE=EQ，∠1=∠2，
∵∠QEM=45°，
∴∠2+∠3=45°，
∴∠1+∠3=45°，
∴∠IEM=∠QEM，
在△EIM和△EQM中，
，
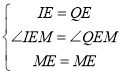∴△EIM=EQM（SAS），
∴IM=MQ，
∴AM-MQ=AM-IM=AI，
由（2）可知OA=OF=3，∠AOF=90°，
∴∠A=∠AEG=45°，
∴PH=GE=GA=IG+AI，
∴AI=GA-IG=PH-QH=PQ，
