题目内容
【题目】已知:⊙O是正方形ABCD的外接圆,点E在![]() 上,连接BE、DE,点F在
上,连接BE、DE,点F在![]() 上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
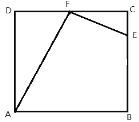
(1)如图1,求证:∠CBE=∠DHG;
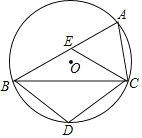
(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;
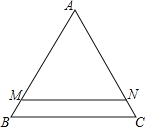
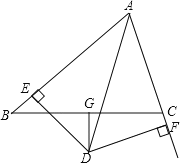
(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER的面积与△DHK的面积的差为![]() ,求线段BR的长.
,求线段BR的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】(1)由正方形的四个角都为直角,得到两个角为直角,再利用同弧所对的圆周角相等及角平分线定义,等量代换即可得证;
(2)如图2,过H作HM⊥KD,垂足为点M,根据题意确定出△BEP≌△HKM,利用全等三角形对应边相等即可得证;
(3)根据3HF=2DF,设出HF=2a,DF=3a,由角平分线定义得到一对角相等,进而得到正切值相等,表示出DM=3a,利用正方形的性质得到△BED≌△DFB,得到BE=DF=3a,过H作HS⊥BD,垂足为S,根据△BER的面积与△DHK的面积的差为![]() ,求出a的值,即可确定出BR的长.
,求出a的值,即可确定出BR的长.
(1)证明:如图1,
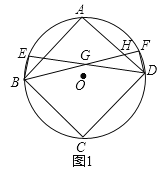
∵四边形ABCD是正方形,
∴∠A=∠ABC=90°,
∵∠F=∠A=90°,
∴∠F=∠ABC,
∵DA平分∠EDF,
∴∠ADE=∠ADF,
∵∠ABE=∠ADE,
∴∠ABE=∠ADF,
∵∠CBE=∠ABC+∠ABE,∠DHG=∠F+∠ADF,
∴∠CBE=∠DHG;
(2)如图2,过H作HM⊥KD,垂足为点M,
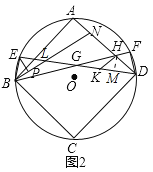
∵∠F=90°,
∴HF⊥FD,
∵DA平分∠EDF,
∴HM=FH,
∵FH=BP,
∴HN=BP,
∵KH∥BN,
∴∠DKH=∠DLN,
∴∠ELP=∠DLN,
∴∠DKH=∠ELP,
∵∠BED=∠A=90°,
∴∠BEP+∠LEP=90°,
∵EP⊥BN,
∴∠BPE=∠EPL=90°,
∴∠LEP+∠ELP=90°,
∴∠BEP=∠ELP=∠DKH,
∵HM⊥KD,
∴∠KMH=∠BPE=90°,
∴△BEP≌△HKM,
∴BE=HK;
(3)解:如图3,连接BD,
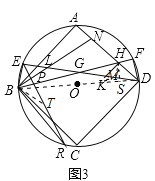
∵3HF=2DF,BP=FH,
∴设HF=2a,DF=3a,
∴BP=FH=2a,
由(2)得:HM=BP,∠HMD=90°,
∵∠F=∠A=90°,
∴tan∠HDM=tan∠FDH,
∴![]() ,
,
∴DM=3a,
∵四边形ABCD为正方形,
∴AB=AD,
∴∠ABD=∠ADB=45°,
∵∠ABF=∠ADF=∠ADE,∠DBF=45°-∠ABF,∠BDE=45°-∠ADE,
∴∠DBF=∠BDE,
∵∠BED=∠F,BD=BD,
∴△BED≌△DFB,
∴BE=FD=3a,
过H作HS⊥BD,垂足为S,
∵tan∠ABH=tan∠ADE=![]() ,
,
∴设AB=3![]() m,AH=2
m,AH=2![]() m,
m,
∴BD=![]() AB=6m,DH=AD-AH=
AB=6m,DH=AD-AH=![]() m,
m,
∵sin∠ADB=![]() ,
,
∴HS=m,
∴DS=![]() =m,
=m,
∴BS=BD-DS=5m,
∴tan∠BDE=tan∠DBF=![]() ,
,
∵∠BDE=∠BRE,∴tan∠BRE=![]() ,
,
∵BP=FH=2a,
∴RP=10a,
在ER上截取ET=DK,连接BT,由(2)得:∠BEP=∠HKD,
∴△BET≌△HKD,
∴∠BTE=∠KDH,
∴tan∠BTE=tan∠KDH,
∴![]() ,即PT=3a,
,即PT=3a,
∴TR=RP-PT=7a,
∵S△BER-S△DHK=![]() ,
,
∴![]() BPER-
BPER-![]() HMDK=
HMDK=![]() ,
,
∴![]() BP(ER-DK)=
BP(ER-DK)=![]() BP(ER-ET)=
BP(ER-ET)=![]() ,
,
∴![]() ×2a×7a=
×2a×7a=![]() ,
,
解得:a=![]() (负值舍去),
(负值舍去),
∴BP=1,PR=5,
则BR=![]() .
.