题目内容
在四边形中,若有一组对角都为90°,另一组对角不相等的四边形我们称它为“垂直”四边形,那么下列说法正确的序号是 . (多填或错填得0分,少填酌情给分).
① “垂直”四边形对角互补; ②“垂直”四边形对角线互相垂直;
③“垂直”四边形不可能成为梯形;④ 以“垂直”四边形的非直角顶点为端点的线段若平分这组对角,那么该“垂直”四边形有两组邻边相等.
① “垂直”四边形对角互补; ②“垂直”四边形对角线互相垂直;
③“垂直”四边形不可能成为梯形;④ 以“垂直”四边形的非直角顶点为端点的线段若平分这组对角,那么该“垂直”四边形有两组邻边相等.
①③④
分析:根据四边形的内角和为360°,可得到①③正确;由于没有给定对角线的限制条件,不能得到②“垂直”四边形对角线互相垂直;利用三角形全等可以判断④正确.
解:根据四边形的内角和为360°,可得“垂直”四边形对角互补,所以①正确;
垂直”四边形对角线不一定互相垂直,②不正确;
因为“垂直”四边形有一组对角都为90°,另一组对角不相等的四边形,根据四边形的内角和为360°可得不能有相邻的角都为90°,则“垂直”四边形不可能成为梯形,所以③正确;
以“垂直”四边形的非直角顶点为端点的线段若平分这组对角,则可以得到被这条线段分成的两个三角形全等,则该“垂直”四边形有两组邻边相等,所以④正确.
故答案为①③④.

练习册系列答案
相关题目

 中,
中, ∥
∥ ,
, 的面积等于9,
的面积等于9,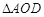 的面积等于6,
的面积等于6, ,求
,求 的长.
的长. 的两条对角线相交于点
的两条对角线相交于点 ,
, ,则矩形的对角线
,则矩形的对角线 的长是( )
的长是( )



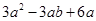 ,一边长为
,一边长为 ,则它的周长是( ).
,则它的周长是( ).


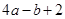
 ∠B=20°,则∠ADE=_____________.
∠B=20°,则∠ADE=_____________.