题目内容
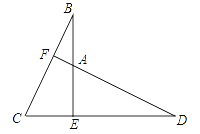
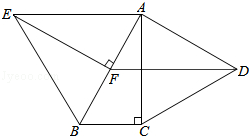
【题目】已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
(1)求点A坐标和⊙P的半径;
(2)求抛物线的解析式;
(3)当△MOB与以点B、C、D为顶点的三角形相似时,求△CDN的面积.
【答案】
(1)
解:如图1所示:过点P作PE⊥BC,垂足为E.

∵PE⊥BC,
∴BE=EC=4.
∴OE=5.
∵⊙P与y轴相切,
∴PA⊥y轴.
∵∠PAO=∠AOE=∠OEP=90°,
∴四边形AOEP为矩形.
∴AP=OE=5,AO=EP.
∴⊙P的半径为5.
在Rt△BEP中,PE= ![]() =
= ![]() =3.
=3.
∴OA=3.
∴点A的坐标为(0,﹣3)
(2)
解:设抛物线的解析式为y=a(x﹣1)(x﹣9),将点A的坐标代入得:9a=﹣3,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2
x2 ![]() x﹣3
x﹣3
(3)
解:如图2所示:当直线MB经过点P时.

∵BD为⊙P的直径,
∴∠BCD=90°.
∴∠BCD=∠MOB=90°.
又∵∠MBO=∠CBD,
∴△MOB∽△DCB.
设MB的解析式为y=kx+b,将点B和点D的坐标代入得 ![]() ,解得:k=﹣
,解得:k=﹣ ![]() ,b=
,b= ![]() .
.
∴直线MB的解析式为y=﹣ ![]() x+
x+ ![]() .
.
将x=9代入得y=﹣6.
∴CD=6.
将y=﹣ ![]() x+
x+ ![]() 与y=﹣
与y=﹣ ![]() x2
x2 ![]() x﹣3联立解得:x=1或x=
x﹣3联立解得:x=1或x= ![]() .
.
△CDN的面积= ![]() DC(xN﹣xD)=
DC(xN﹣xD)= ![]() ×6×
×6× ![]() =
= ![]()
【解析】(1)过点P作PE⊥BC,垂足为E,连结AP.依据垂径定理可知BE=EC=4则OE=5,然后再证明四边形AOEP为矩形可求得到AP=OE=5,在Rt△BEP中,依据勾股定理可求得PE的长;(2)设抛物线的解析式为y=a(x﹣1)(x﹣9),将点A的坐标代入求解即可;(3)△MOB为直角三角形,则△BDC为直角三角形,故此只存在∠BCD为直角的情况,则MB经过点P,然后求得MB的解析式,将直线BM的解析式与抛物线的解析式组成方程组可求得点N的坐标,然后依据CD∥y轴可求得点CD的长,最后依据△CDN的面积= ![]() DC(xN﹣xD)求解即可.
DC(xN﹣xD)求解即可.

 名校课堂系列答案
名校课堂系列答案