题目内容
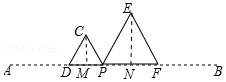
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示. 
(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
【答案】
(1)解:∵△CDP和△EFP是等边三角形,
∴CD=PC=PD,EF=EP=PF,AP=3PD,BP=3PF,
∵DF=PD+PF=2,
∴AB=AP+BP=3DF=3×2=6
(2)解:没有最大值,理由如下:
设CD=PC=PD=x,则EF=EP=PF= ![]() (18﹣3x)=6﹣x,
(18﹣3x)=6﹣x,
作CM⊥PD于M,EN⊥PF于N,
则DM= ![]() PD=
PD= ![]() x,PN=
x,PN= ![]() PF=
PF= ![]() (6﹣x),
(6﹣x),
∴CM= ![]() DM=
DM= ![]() x,EN=
x,EN= ![]() (6﹣x),
(6﹣x),
∴△CDP的面积= ![]() PDCM=
PDCM= ![]() x2,△EFP的面积=
x2,△EFP的面积= ![]() (6﹣x)2,
(6﹣x)2,
∴等边△CDP和△EFP的面积之和S= ![]() x2+
x2+ ![]() (6﹣x)2=
(6﹣x)2= ![]() x2﹣3
x2﹣3 ![]() x+9
x+9 ![]() ,
,
∵ ![]() >0,
>0,
∴S有最小值,没有最大值.
【解析】(1)由等边三角形的性质容易得出结果;(2)设CD=PC=PD=x,则EF=EP=PF=6﹣x,求出等边△CDP和△EFP的面积之和S= ![]() x2﹣3
x2﹣3 ![]() x+9
x+9 ![]() ,
, ![]() >0,得出S有最小值,没有最大值.
>0,得出S有最小值,没有最大值.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a),还要掌握等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)的相关知识才是答题的关键.

【题目】为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.