题目内容
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 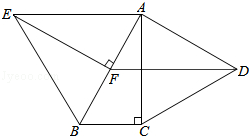
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
【答案】
(1)证明:∵△ABE是等边三角形,EF⊥AB,
∴∠EAF=60°,AE=BE,∠EFA=90°.
又∵∠ACB=90°,∠ABC=60°,
∴∠EFA=∠ACB,∠EAF=∠ABC.
在△ABC和△EAF中 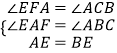 ,
,
∴△ABC≌△EAF
(2)解:结论:四边形EFDA是平行四边形.
理由:∵△ABC≌△EAF,
∴EF=AC.
∵△ACD是的等边三角形,
∴AC=AD,∠CAD=60°,
∴AD=EF.
又∵Rt△ABC中,∠ABC=60°,∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=90°,
∴∠EFA=∠BAD=90°,
∴EF∥AD.
又∵EF=AD,
∴四边形EFDA是平行四边形
【解析】(1)由△ABE是等边三角形可知:AE=BE,∠EAF=60°,于是可得到∠EFA=∠ACB,∠EAF=∠ABC,接下来依据AAS证明△ABC≌△EAF即可;(2)由△ABC≌△EAF可得到EF=AC,由△ACD是的等边三角形进而可证明AC=AD,然互再证明∠BAD=90°,可证明EF∥AD,故此可得到四边形EFDA为平行四边形.

【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题: 某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | 30% |
B.文学类 | n | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
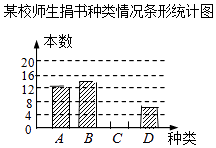
(1)统计表中的n= , 并补全条形统计图;
(2)本次活动师生共捐书2000本,请估计有多少本科普类图书?