题目内容
【题目】为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题:
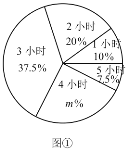
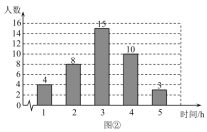
(Ⅰ)该校抽查九年级学生的人数为_________,图①中的m值为_________;
(Ⅱ)求统计的这组数据的众数、中位数和平均数.
(Ⅲ)根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于![]() 的学生人数.
的学生人数.
【答案】(I)40,25 ;(Ⅱ)平均数:3;众数为3;中位数为3;(III)280人.
【解析】
(Ⅰ)由1小时的人数及其占总人数的百分比可得总人数,用4小时的人数除以总人数即可求出m;
(Ⅱ)根据众数、中位数及加权平均数的定义可得答案;
(Ⅲ)用总人数乘以每周平均课外阅读时间大于2h的学生人数所占的百分比即可.
(Ⅰ)该校抽查九年级学生的人数为:4÷10%=40(人),
∵m%=![]() ×100%=25%,
×100%=25%,
∴m=25,
故答案为:40,25;
(Ⅱ)平均数:![]() .
.
∵在这组样本数据中,3出现了15次,出现的次数最多,
∴这组样本数据的众数为3.
∵将这组样本数据按从小到大的顺序排列,
其中处于中间的两个数都是3,有![]() ,
,
∴这组样本数据的中位数为3.
(III)![]() ,
,
∴根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于![]() 的约有280人.
的约有280人.

 探究与巩固河南科学技术出版社系列答案
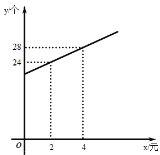
探究与巩固河南科学技术出版社系列答案【题目】已知二次函数 y=ax2+bx+c,其中 y 与 x 的部分对应值如表:
x | -2 | -1 | 0.5 | 1.5 |
y | 5 | 0 | -3.75 | -3.75 |
下列结论正确的是( )
A.abc<0B.4a+2b+c>0
C.若 x<-1 或 x>3 时,y>0D.方程 ax2+bx+c=5 的解为 x1=-2,x2=3
【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.