题目内容
如图,在梯形ABCD中,AD∥BC,且AD>BC,BC=6cm,AD=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,其中一个动点到达终点时,另一个动点也停止运动.试计算,
(1)当运动时间为多少时,直线PQ四边形截出四边形是一个平行四边形?
(2)在直线PQ所截出的平行四边形中,在PQ的对边任取一点O,连接OP、OQ,得到△OPQ,则△OPQ的面积与直线PQ所截出的平行四边形的面积有何关系?并说明理由.(在图1、图2中任取一种画出图形,说明理由即可.)

(1)当运动时间为多少时,直线PQ四边形截出四边形是一个平行四边形?
(2)在直线PQ所截出的平行四边形中,在PQ的对边任取一点O,连接OP、OQ,得到△OPQ,则△OPQ的面积与直线PQ所截出的平行四边形的面积有何关系?并说明理由.(在图1、图2中任取一种画出图形,说明理由即可.)

(1)设运动时间为t秒时,直线PQ四边形截出四边形是一个平行四边形,
①当AP=BQ时,AP=t,BQ=6-2t,
∴t=6-2t,
解得t=2,
②当PD=CQ时,AP=9-t,CQ=2t,
∴9-t=2t,
解得t=3秒,
此时点Q与点B重合,符合题意,
∴当运动时间为2秒或3秒时,直线PQ四边形截出四边形是一个平行四边形;
(2)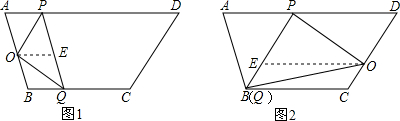 △OPQ的面积平行四边形的面积的一半.
△OPQ的面积平行四边形的面积的一半.
理由如下:如图1,过点O作OE∥AP,
则OE∥AP且OE=AP,
OE∥BQ且OE=BQ,
∴四边形AOEP与四边形OBQE都是平行四边形,
∴S△OPE=
S平行四边形AOEP,
S△OQE=
S平行四边形OBQE,
∴S△OPE+S△OQE=
S平行四边形AOEP+
S平行四边形OBQE=
S平行四边形ABQP,
即S△OPQ=
S平行四边形ABQP,
同理可证,图2中S△OPQ=
S平行四边形PQCD.
①当AP=BQ时,AP=t,BQ=6-2t,
∴t=6-2t,
解得t=2,
②当PD=CQ时,AP=9-t,CQ=2t,
∴9-t=2t,
解得t=3秒,
此时点Q与点B重合,符合题意,
∴当运动时间为2秒或3秒时,直线PQ四边形截出四边形是一个平行四边形;
(2)
 △OPQ的面积平行四边形的面积的一半.
△OPQ的面积平行四边形的面积的一半.理由如下:如图1,过点O作OE∥AP,
则OE∥AP且OE=AP,
OE∥BQ且OE=BQ,
∴四边形AOEP与四边形OBQE都是平行四边形,
∴S△OPE=
| 1 |
| 2 |
S△OQE=
| 1 |
| 2 |
∴S△OPE+S△OQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即S△OPQ=
| 1 |
| 2 |
同理可证,图2中S△OPQ=
| 1 |
| 2 |

练习册系列答案
相关题目
 ),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
 EC、BF、CF.
EC、BF、CF.
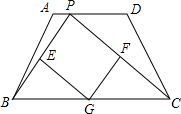

 于AB,AC于点E,点F,下列结论正确的是( )
于AB,AC于点E,点F,下列结论正确的是( )