题目内容
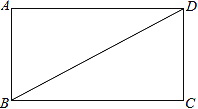
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.


【答案】 36 17
【解析】试题分析:(1)由直角三角形两直角边的平方和等于斜边的平方变形计算得出;
(2)
试题解析:
(1)BC2=AB2-AC2=100-64=36,
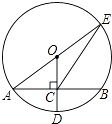
(2)如图所示:作点P关于AC的对称点P’,连接P’D交AC于点M,则点M即为所求,此时有MP+MD最小值,即为P’D的长度.
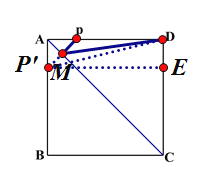
过点P’作P’E![]() CD于点E,
CD于点E,
∵正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]()
∴P’E=4,DE=A P’=AP=1
∴DP’2=DE2+P’E2=16+1=17.

练习册系列答案
相关题目