Question

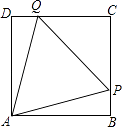
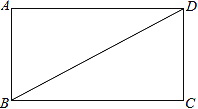
【题目】如图，BD是矩形ABCD的一条对角线．

（1）作BD的垂直平分线EF，分别交AD、BC于点E、F，垂足为点O（用尺规作图，保留作图痕迹，不要求写作法）；

（2）求证：AF=CE．

Answer 1

【答案】见解析

【解析】

（1）利用基本作图作线段BD的垂直平分线即可；

（2）先证明△DOE≌△BOF得到DE=BF，然后证明四边形AECF为平行四边形，从而得到AF=CE．

（1）解：如图，EF为所作；

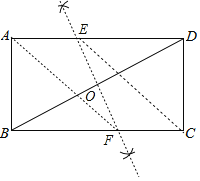
（2）证明：∵四边形ABCD为平行四边形，

∴AD=BC，AD∥BC，

∴∠ADB=∠CBD，

∵EF垂直平分BD，

∴BO=OD，

在△DOE和△BOF中

，

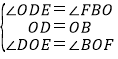∴△DOE≌△BOF，

∴DE=BF，

∴AE=CF，

而AE∥CF，

∴四边形AECF为平行四边形，

∴AF=CE．