Question

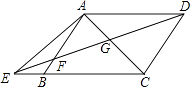
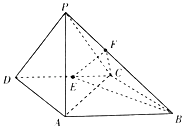
【题目】如图，在四棱锥P﹣ABCD中，侧面PAD⊥底面ABCD，底面ABCD是平行四边形，∠ABC=45°，AD=AP=2，AB=DP=2 ，E为CD的中点，点F在线段PB上．
（Ⅰ）求证：AD⊥PC；
（Ⅱ）当三棱锥B﹣EFC的体积等于四棱锥P﹣ABCD体积的 时，求 的值．

Answer 1

【答案】（I）证明：连接AC，∵BC=AD=2，AB=2 ，∠ABC=45°， ∴AC= =2，
∴AC2+BC2=AB2 ， ∴AC⊥BC，
又AD∥BC，∴AD⊥AC，
∵AD=AP=2，DP=2 ，∴AD⊥AP，
又AP平面APC，AC平面APC，AP∩AC=A，
∴AD⊥平面PAC，又PC平面APC，
∴AD⊥PC．
（II）解：∵侧面PAD⊥底面ABCD，
侧面PAD∩底面ABCD=AD，AD⊥PA，PA平面PAD，
∴PA⊥平面ABCD，
∴VP﹣ABCD= ，
设F到平面ABCD的距离为h，则
VB﹣CEF=VF﹣BCE= = ，
∴ = VP﹣ABCD= ，
∴h= ，
∴ = = ，
∴ = ．

【解析】（I）利用勾股定理的逆定理证明AD⊥AP，AC⊥BC，从而AD⊥平面PAC，于是AD⊥PC；（II）利用面面垂直的性质证明PA⊥平面ABCD，根据棱锥的体积关系得出F到平面ABCD的距离，从而得出 的值．
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点，需要掌握垂直于同一个平面的两条直线平行才能正确解答此题．