题目内容
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
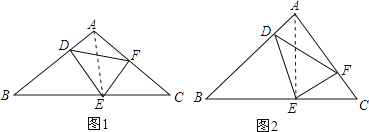
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).
【答案】
(1)
解:如图1,连结AE.
∵DE=DF,
∴∠DEF=∠DFE,
∵∠ADF+∠DEC=180°,
∴∠ADF=∠DEB.
∵∠AFE=∠BDE,
∴∠AFE+∠ADE=180°,
∴A、D、E、F四点共圆,
∴∠DAE=∠DFE=∠DEF,∠ADF=∠AEF.
∵∠ADF=∠DEB=∠AEF,
∴∠AEF+∠AED=∠DEB+∠AED,
∴∠AEB=∠DEF=∠DFE=∠BAE,
∴AB=BE.
(2)
解:如图2,连结AE.
∵∠AFE=∠BDE,
∴∠AFE+∠ADE=180°,
∴A、D、E、F四点共圆,
∴∠ADF=∠AEF,
∵∠DAF=90°,
∴∠DEF=90°,
∵∠ADF+∠DEC=180°,
∴∠ADF=∠DEB.
∵∠ADF=∠AEF,
∴∠DEB=∠AEF.
在△BDE与△AFE中,
![]() ,
,
∴△BDE∽△AFE,
∴![]() .
.
在直角△DEF中,∵∠DEF=90°,DE=kDF,
∴EF=![]() =
=![]() DF,
DF,
∴![]() =
=![]() =
=![]() ,
,
∴BD=![]() .
.
【解析】(1)如图1,连结AE.先由DE=DF,得出∠DEF=∠DFE,由∠ADF+∠DEC=180°,得出∠ADF=∠DEB.由∠AFE=∠BDE,得出∠AFE+∠ADE=180°,那么A、D、E、F四点共圆,根据圆周角定理得出∠DAE=∠DFE=∠DEF,∠ADF=∠AEF.再由∠ADF=∠DEB=∠AEF,得出∠AEF+∠AED=∠DEB+∠AED,则∠AEB=∠DEF=∠BAE,根据等角对等边得出AB=BE;
(2)如图2,连结AE.由A、D、E、F四点共圆,得出∠ADF=∠AEF,由∠DAF=90°,得出∠DEF=90°,再证明∠DEB=∠AEF.又∠AFE=∠BDE,根据两角对应相等的两三角形相似得出△BDE∽△AFE,利用相似三角形对应边成比例得到![]() =
=![]() .在直角△DEF中,利用勾股定理求出EF=
.在直角△DEF中,利用勾股定理求出EF=![]() =
=![]() DF,然后将AF=m,DE=kDF代入,计算即可求解.
DF,然后将AF=m,DE=kDF代入,计算即可求解.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 | 测试成绩(分) | 人数 |
优秀 | 45≤x≤50 | 140 |
良好 | 37.5≤x<45 | 36 |
及格 | 30≤x<37.5 | |
不及格 | x<30 | 6 |

根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有人,达到优秀的人数占本次测试总人数的百分比为%.
(2)本次测试的学生数为人,其中,体质健康成绩为及格的有人,不及格的人数占本次测试总人数的百分比为%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.