题目内容
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.

【答案】(1)证明见解析;(2)![]() ;(3)△CB′F周长的最小值为
;(3)△CB′F周长的最小值为![]() .
.
【解析】(1)利用正方形的性质即可证得结论;(2)运用翻折的性质在Rt△B′MF中运用勾股定理BF的长;(3)根据折叠的对称性求出△CB′F周长的最小值.
(1)证明:
∵ABCD是正方形,
∴∠B=90°,AB=BC,
∵∠BEF=45°,
∴∠BFE=∠BEF=45°,
∴BE=BF,
∴AE=CF.
(2)如图1,过B′点作GH∥AD,分别交AB、CD于点G、H,则∠B′GE=90°.
∵B′C=B′D,
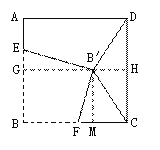
∴DH=AG=![]() DC=8,
DC=8,
∵AE=3,AB=16,
∴BE=13,
由翻折的性质可得:B′E=BE=13.
∴ EG=AG﹣AE=8﹣3=5,
∴ B′G=![]() ,
,
过B′点作B′M∥BC交BC于点M,
则B′M=BG=8.BM=B′G=12,
设BF= ![]() ,则B′F=BF=
,则B′F=BF= ![]() ,FM=12﹣
,FM=12﹣![]() ,
,
在Rt△B′MF中,∠B′MF=90°,
∴ B′F2= FM2+ B′M2,
即![]() ,
,
解得: ![]() ,即BF =
,即BF =![]() .
.
(3)如图2.
∵FB′+ FC=BC=16,
∴当CB′最小时,△CB′F的周长也最小,

而当C、B′、E三点共线时,CB′取最小值,
此时CB′=CE-EB′=![]() ,
,
∴△CB′F周长的最小值为![]() .
.
或∵FB′+ FC=BC=16,
∴当CB′最小时,△CB′F的周长也最小,
当∠CB′F=90°时,CB′最小,
而这时C、B′、E三点共线,
此时CB′=CE-EB′=![]() ,
,
∴△CB′F周长的最小值为![]() .
.
“点睛”本题考查了正方形的性质、翻折的性质、折叠的对称性,灵活运用性质是解题的关键.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案