题目内容
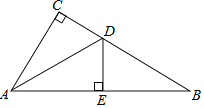
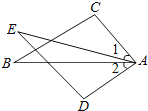
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() ,
,![]() 的面积为14.将
的面积为14.将![]() 沿
沿![]() 轴平移得到
轴平移得到![]() ,当点
,当点![]() 为
为![]() 中点时,点
中点时,点![]() 恰好在
恰好在![]() 轴上.
轴上.

求:(1)点![]() 的坐标;
的坐标;
(2)![]() 的面积.
的面积.
【答案】(1) F(0,7);(2) S△EOF=14.
【解析】
(1)根据点A的坐标、AB的长度求出点B的坐标,再利用△ABC的面积求出点C的纵坐标,然后根据点F在y轴上解答即可;
(2)根据点D是AB的中点与点A、B的坐标求出点D的坐标,再求出AD的长度,根据平移的性质求出OE的长度,然后根据三角形的面积公式列式进行计算即可得解.
(1)∵A(10,0),AB=4,
∴B(6,0),
∵S△ABC=![]() AB|yC|=14,
AB|yC|=14,
∴|yC|=7,
∵点C在第二象限,
∴|yC|=7,
∵△ABC沿x轴平移得到△DEF,
∴F(0,7);
(2)∵A(10,0),B(6,0),D为AB中点,
∴D(8,0),AD=BE=2,
∴E(4,0),
∴OE=4,
∴S△EOF=![]() OEOF=
OEOF=![]() ×4×7=14.
×4×7=14.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目