题目内容
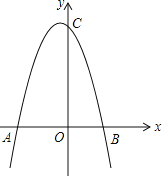
【题目】如图,二次函数y=ax2+bx+2(a≠0)的图象与x 轴交于A,B 两点,与y 轴交于点C,已知点 A(-4,0),B(1,0).
(1)求抛物线的解析式;
(2)若点 D(m,n) 是抛物线在第二象限的部分上的一动点,四边形 ![]() 的面积为
的面积为 ![]() ,求
,求 ![]() 关于 m 的函数关系;
关于 m 的函数关系;
(3)若点 E 为抛物线对称轴上任意一点,当以 A,C,E 为顶点的三角形是直角三角形时,请求出满足条件的所有点 E 的坐标.

【答案】(1)![]()
(2) ![]()
(3) 
【解析】试题解析:(1)用待定系数法求出函数解析式即可;(2)用m表示出点D的坐标,过点D作DH⊥x轴于点H,利用四边形OCDA的面积=△ADH的面积+ 四边形OCDH的面积即可求得S关于 m 的函数关系;(3)求出函数的对称轴,设出点E的坐标,分∠AEC=90°、
∠ACE=90°和∠CAE=90°三种情况求点E的坐标即可.
试题分析:
(1)∵A(-4,0),B(1,0) 在二次函数y=ax2+bx+2(a≠0)的图象上,
∴![]() , 解得
, 解得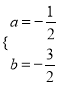 .
.
∴抛物线的解析式为![]() .
.
(2)∵ 点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m, ![]() ),
),
过点D作DH⊥x轴于点H,
则DH=![]() ,AH=m+4,HO=-m,
,AH=m+4,HO=-m,
∵ 四边形OCDA的面积=△ADH的面积+ 四边形OCDH的面积,
∴![]() ,
,
化简,得![]() .
.
(3) 抛物线![]() 的对称轴为
的对称轴为![]() ,
,
故设点E的坐标为(![]() ).
).
∴![]() .
.
若∠AEC=90°,则![]() ,
,
解得![]() ,
,
此时点E的坐标是 或
或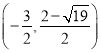 ;
;
若∠ACE=90°,则![]() ,
,
解得n=5,此时点E的坐标是![]() ;
;
若∠CAE=90°,则![]() ,
,
解得 n=-5,此时点E的坐标是![]() ;
;
综上所述点E的坐标是 或
或 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目