题目内容
【题目】如图,在Rt△ABC中,∠C=90°.AD是△ABC的角平分线,若CD=4,AC=12,AB=15,DE⊥AB于E,则△BDE的面积是______.
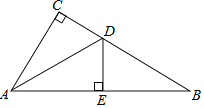
【答案】6.
【解析】
先根据角平分线的性质得出CD=ED,再利用HL证明Rt△ACD≌Rt△AED,根据全等三角形的性质得到AE=AC=12,DE=CD=4,于是得到BE=AB-AE=3,进而根据三角形的面积公式即可求出△BDE的面积.
∵∠C=90°,AD是△ABC的角平分线,DE⊥AB,
∴CD=ED.
在Rt△ACD与Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=12,DE=CD=4,
∵AB=15,
∴BE=AB-AE=3,
∴S△BDE=![]() BEDE=
BEDE=![]() ×3×4=6.
×3×4=6.
故答案为6.

练习册系列答案
相关题目