题目内容
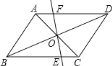
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
①根据四边形ABCD是矩形,BE⊥AC,可得∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②根据点E是AD边的中点,以及AD∥BC,得出△AEF∽△CBF,根据相似三角形对应边成比例,可得CF=2AF,故②正确;
③根据△AEF∽△CBF得到EF与BF的比值,据此求出S△AEF=![]() S△ABF,S△AEF=
S△ABF,S△AEF=![]() S△BCF,可得S△AEF:S△CAB=1:6,故③错误;
S△BCF,可得S△AEF:S△CAB=1:6,故③错误;
④根据AA可得△AEF∽△BAF,根据相似三角形的性质可得AF2=2EF2,故④正确.
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
∴∠EAC=∠ACB,
∵BE⊥AC,
∴∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() =
=![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,
,
∴CF=2AF,故②正确;
∵△AEF∽△CBF,
∴EF:BF=1:2,
∴S△AEF=![]() S△ABF,S△AEF=
S△ABF,S△AEF=![]() S△BCF,
S△BCF,
∴S△AEF:S△CAB=1:6,故③错误;
∵△AEF∽△CAB,
∴∠AEF=∠BAF,
∵∠AFE=∠BFA=90°,
∴△AEF∽△BAF,
∴![]() ,
,
AF2=EFBF=2EF2,故④正确.
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目