Question

【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°， 点D为射线CB上一点，且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上，截取AE=AD(点E与点C在直线AD的同侧)，连接CE.

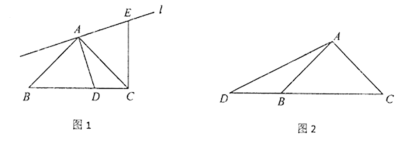
（1）当点D在线段CB上时，如图1,线段CE与BD的数量关系为____________，位置关系为___________；

（2）当点D在线段CB的延长线上时，如图2,

①请将图形补充完整;

②（1）中的结论是否仍成立?如果成立，请证明;如果不成立，请说明理由.

Answer 1

【答案】（1）CE=BD, CE⊥BD；（2）①见解析，②成立，理由见解析

【解析】

（1）在图1中证明△ABD≌△ACE，得到CE=BD，∠B=∠ACE=45°即可得到∠BCE=90°，即CE⊥BD；

（2）①根据题意，画出图形即可；

②与（1）同理，证明△ADB≌△AEC，然后得到CE=BD，然后得到∠ABC=∠ACB=45°，然后得到∠BCE=90°，即CE⊥BD.

证明：（1）∵AD⊥l，

∴∠DAE=∠BAC=90°，

∴∠BAD+∠DAC=∠DAC+∠CAE=90°，

∴∠BAD=∠CAE，

∵AD=AE，AB=AC，

∴△ABD≌△ACE，

∴CE=BD，∠B=∠ACE=45°，

∴∠ACB+∠ACE=45°+45°=90°，

∴∠BCE=90°，即CE⊥BD；

故答案为：CE=BD，CE⊥BD；

（2）①补全图形，如图：

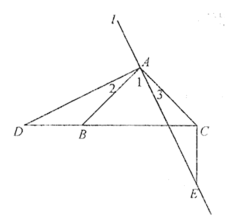
②CE=BD，CE⊥BD仍成立；

证明：∵AD⊥AE

∴∠DAE=90°

∵∠BAC=90°

∴∠DAE∠1=∠BAC∠1

即∠2=∠3

∵AB=AC, AD=AE

∴△ADB≌△AEC

∴CE=BD，∠ACE=∠ABD

∵∠ABC=∠ACB=45°

∴∠ACE=∠ABD=135°

∴∠DCE=∠ACE∠ACB=90°

∴CE⊥BD.