题目内容
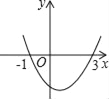
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
【答案】D
【解析】分析:首先根据二次函数图象开口方向可得a>0,根据图象与y轴交点可得c<0,再根据二次函数的对称轴x=-![]() ,结合图象与x轴的交点可得对称轴为x=1,结合对称轴公式可判断出①的正误;根据对称轴公式结合a的取值可判定出b<0,根据a、b、c的正负即可判断出②的正误;利用抛物线与x轴有两个交点即可判断出③的正误;利用当x=4时,y>0,则16a+4b+c>0,由①知,b=-2a,得出8a+c>0,即可判断出④的正误.
,结合图象与x轴的交点可得对称轴为x=1,结合对称轴公式可判断出①的正误;根据对称轴公式结合a的取值可判定出b<0,根据a、b、c的正负即可判断出②的正误;利用抛物线与x轴有两个交点即可判断出③的正误;利用当x=4时,y>0,则16a+4b+c>0,由①知,b=-2a,得出8a+c>0,即可判断出④的正误.
详解:根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,
对称轴:x=![]() >0,
>0,
①∵它与x轴的两个交点分别为(1,0),(3,0),
∴对称轴是x=1,
∴![]() =1,
=1,
∴b+2a=0,
故①正确;
②∵a>0,![]() =1,
=1,
∴b<0,
又∵c<0,
∴abc>0,
故②错误;
③∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,
由①知,b=2a,
∴8a+c>0;
故④正确;
综上所述,正确的结论是:①③④,
故选D.

【题目】我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别 | 投进个数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
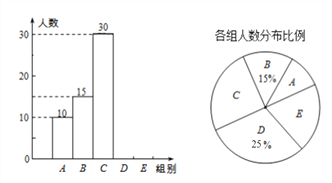
根据以上信息完成下列问题。
①本次抽取的学生人数为多少?
②统计表中的m=__________;
③扇形统计图中E组所占的百分比;
④补全频数分布直方图;
⑤扇形统计图中“C组”所对应的圆心角的度数;
⑥本次比赛中投篮个数的中位数落在哪一组;
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数.