题目内容
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.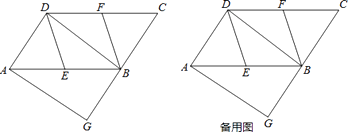
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形;
(3)请利用备用图分析,在(2)的条件下,若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,求PF+PM的最小值,并求出此时线段BP的长.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、CD的中点,
∴DF=BE,又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE∥BF
(2)
证明:∵AG∥DB,AD∥CG,
∴四边形AGBD是平行四边形,
∵∠G=90°,
∴平行四边形AGBD是矩形,
∴∠ADB=90°,又E为边AB的中点,
∴ED=EB,又四边形DEBF是平行四边形,
∴四边形DEBF是菱形
(3)
解:连接EF,连接EM交BD于P,

∵四边形DEBF是菱形,
∴点E和点F关于BD轴对称,此时PF+PM的值最小,
∵四边形DEBF是菱形,∠DEB=120°,
∴∠EBF=60°,
∴△BEF是等边三角形,又BE=4,
∴EM=2 ![]() ,即PF+PM的最小值为2
,即PF+PM的最小值为2 ![]() ,
,
由题意得,点P为△EBF的重心,
∴BP= ![]() .
.
【解析】(1)根据平行四边形的性质得到DF=BE,AB∥CD,根据平行四边形的判定定理证明四边形DEBF是平行四边形,根据平行四边形的性质证明结论;(2)根据矩形的判定定理得到四边形AGBD是矩形,根据直角三角形的性质得到ED=EB,证明结论;(3)连接EM交BD于P,根据轴对称的性质证明此时PF+PM的值最小,根据等边三角形的性质计算即可.
【考点精析】本题主要考查了平行四边形的性质和菱形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


