题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
【答案】
(1)
解:如图,判断3正确.理由如下:
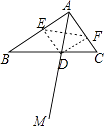
∵∠BAC=90°,DE⊥ABDF⊥AC,
∴DE=DF,∴∠AED=∠AFD=∠EAF=90°,
∴四边形AEDF是矩形,∵DE=DF,
∴四边形AEDF是正方形,
∴AD与EF互相垂直平分.
故判断3正确
(2)
解:①结论:△BCN是等腰直角三角形.理由如下:
如图作NE⊥AB于E,FN⊥AC于F.
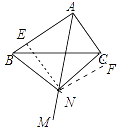
∵MA是∠BAC的平分线,
∴NE=NF,
在Rt△NEB和Rt△NFC中,
![]() ,
,
∴△NEB≌△NFC,
∴BE=CF,∠BNE=∠CNF,
易知四边形AENF是正方形,
∴AE=AF,∠BNC=∠ENF=90°,
∴△BNC是等腰直角三角形.
②∵AB+AC=(AE+BE)+(AF﹣CF)=2AE=18,
∴AE=AF=9,
∵△NEB≌△NFC,
∴S△NEB=S△NFC,
∴S四边形ABNC=S正方形AENF=92=81
【解析】(1)结论:判断3正确.只要证明四边形AEDF是正方形即可解决问题.(2)①△BCN是等腰直角三角形.如图作NE⊥AB于E,FN⊥AC于F.只要证明△NEB≌△NFC,四边形AENF是正方形即可解决问题.②由△NEB≌△NFC,推出S△NEB=S△NFC , 推出S四边形ABNC=S正方形AENF , 由此即可解决问题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案