题目内容
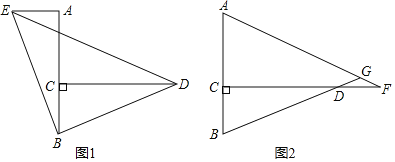
【题目】如图1,已知AB⊥CD,C是AB上一动点,AB=CD
(1)在图1中,将BD绕点B逆时针方向旋转90°到BE,若连接DE,则△DBE为等腰直角三角形;若连接AE,试判断AE与BC的数量和位置关系并证明;
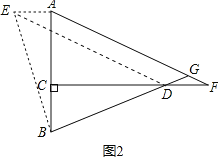
(2)如图2,F是CD延长线上一点,且DF=BC,直线AF,BD相交于点G,∠AGB的度数是一个固定值吗?若是,请求出它的度数;若不是,请说明理由.
【答案】(1)AE=BC,AE⊥BC,证明见解析;(2)∠AGB的度数是固定值,度数为45°.
【解析】
(1)结论:AE=BC,AE⊥BC.根据角的和差关系可得∠ABE=∠BDC,利用SAS证明△ABE≌△BDC,再利用全等三角形的性质得出AE=BC,∠BAE=∠BCD=90°,即可解决问题;
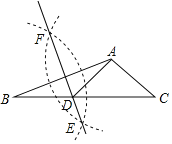
(2)如图,作AE⊥AB于A,使AE=BC,连结DE,BE.利用SAS可证明△ABE≌△BDC,再利用全等三角形的性质得出BE=BD,∠EBD=90°,可得出∠EDB=∠AGB=45°.即可得答案.
(1)结论:AE=BC,AE⊥BC.理由如下:
∵AB⊥CD,将BD绕点B逆时针方向旋转90°到BE,
∴∠BCD=∠EBD=90°,
∴∠ABE+∠DBC=90°,∠DBC+∠BDC=90°,
∴∠ABE=∠BDC,
在△ABE和△CDB中, ,
,
∴△ABE≌△CDB(SAS),
∴AE=BC,∠BAE=∠BCD=90°,
∴AE⊥BC,
∴AE与BC的数量和位置关系是AE=BC,AE⊥BC.
(2)∠AGB的度数是固定值,∠AGB=45°.理由如下:
如图,作AE⊥AB于A,使AE=BC,连结DE,BE.
∵AE⊥AB,∠BCD=90°,
∴∠BAE=∠BCD=90°,
在Rt△BAE和Rt△DCB中, ,
,
∴△BAE≌△DCB(SAS),
∴BE=BD,∠ABE=∠BDC,
∵∠BDC+∠DBC=90°,
∴∠ABE+∠DBC=90°,
∴∠EBD=90°,
∴△BED是等腰直角三角形,
∴∠EDB=45°
∵∠BAE=∠ACD=90°,
∴AE∥DF,
∵AE=BC,BC=DF,
∴AE=DF,
∴四边形AFDE是平行四边形,
∴AF∥DE
∴∠AGB=∠EDB=45°.
∴∠AGB的度数是固定值,∠AGB=45°.