Question

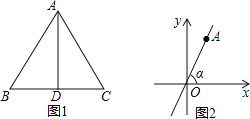
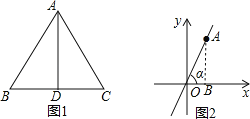
【题目】如图1，AD为正△ABC的高．

（1）利用此图形填表：

	30°	60°
sin
cos
tan

（2）利用（1）题中结论，计算：（）﹣1﹣3tan60°+

（3）利用（1）题中结论解答：如图2，直线l：y=x与x轴所夹的锐角为α，直线l上点A的横坐标为1，求∠α．

Answer 1

【答案】（1），，，，，；（从左向右排列）（2）2；（3）∠α=60°．

【解析】

试题分析：（1）设△ABC的边长为2a，如图1，根据等边三角形的性质得到∠BAD=30°，BD=a，再利用勾股定理计算出AD=a，然后根据锐角三角函数的定义求30°和60°的锐角三角函数值；

（2）根据负整数指数幂和特殊角的三角函数值得到原式=2﹣3+3，然后合并即可；

（3）作AB⊥x轴于B，如图2，利用一次函数图象上点的坐标特征求出A（1，），则OB=1，AB=，再计算出∠α的正切值，然后根据特殊角的三角函数值得到∠α的度数．

解：（1）设△ABC的边长为2a，如图1，

∵AD⊥BC，

∴∠BAD=30°，BD=a，

∴AD==a，

∴sin∠BAD=sin30°===，则cosB=cos60°=；

cos∠BAD=cos30°===，则sinB=sin60°=；

tan∠BAD=tan30°===，则tanB=tan60°===；

故答案为，，，，，；（从左向右排列）

（2）原式=2﹣3+3

=2；

（3）作AB⊥x轴于B，如图2，

当x=1时，y=x=，则A（1，），

∴OB=1，AB=，

在Rt△AOB中，tanα==，

∴∠α=60°．