题目内容
【题目】如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（ ）
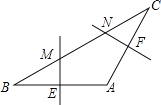
A．4cm B．3cm C．2cm D．1cm
【答案】C
【解析】
试题分析：连接AM、AN、过A作AD⊥BC于D，求出AB、AC值，求出BE、CF值，求出BM、CN值，代入MN=BC﹣BM﹣CN求出即可．
解：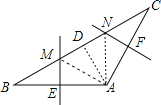
连接AM、AN、过A作AD⊥BC于D，
∵在△ABC中，AB=AC，∠A=120°，BC=6cm，
∴∠B=∠C=30°，BD=CD=3cm，
∴AB=
=2
cm=AC，
∵AB的垂直平分线EM，
∴BE=
AB=cm
同理CF=
cm，
∴BM=
=2cm，
同理CN=2cm，
∴MN=BC﹣BM﹣CN=2cm，
故选C．
练习册系列答案
走进文言文系列答案
相关题目
【题目】如图1，AD为正△ABC的高．
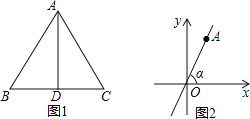
（1）利用此图形填表：
30° | 60° | |
sin | ||
cos | ||
tan |
（2）利用（1）题中结论，计算：（
）﹣1﹣3tan60°+
（3）利用（1）题中结论解答：如图2，直线l：y=
x与x轴所夹的锐角为α，直线l上点A的横坐标为1，求∠α．