题目内容
【题目】如图,在△ABC中,AB=5,AC=6,BC=7,点D,E分别在AB,AC上,DE∥BC.
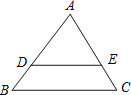
(1)当AD:DB=4:3时,求DE长;
(2)当△ADE的周长与四边形BCED的周长相等,求DE的长.
【答案】(1)DE=4;(2)DE=![]() .
.
【解析】
试题分析:(1)由DE∥BC,可得△ADE∽△ABC,然后由相似三角形的对应边成比例,求得DE长;
(2)由△ADE的周长与四边形BCED的周长相等,设AE+AD=a,CE+DB=b,可得![]() ,继而求得a的值,即AE+AD=9①,又由△ADE∽△ACB,根据相似三角形的对应边成比例,可得
,继而求得a的值,即AE+AD=9①,又由△ADE∽△ACB,根据相似三角形的对应边成比例,可得![]() ②,继而求得AE的长,进而求得答案.
②,继而求得AE的长,进而求得答案.
解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴![]() =
=![]() ,
,
∵AD:DB=4:3,
∴AD:AB=4:7,
∵BC=7,
∴DE=4;
(2)∵△ADE的周长与四边形BCED的周长相等,
∴AD+AE+ED=BC+EC+DE+DB,即AE+AD=BC+CE+DB,
设AE+AD=a,CE+DB=b,则![]() ,
,
解得:a=9,
即AE+AD=9①,
∵△ADE∽△ACB,
∴![]() ②,
②,
由①②,得到AE=![]() ,
,
∵![]() ,
,
∴DE=![]() .
.

练习册系列答案
相关题目
【题目】如图1,AD为正△ABC的高.
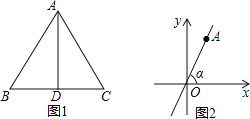
(1)利用此图形填表:
30° | 60° | |
sin | ||
cos | ||
tan |
(2)利用(1)题中结论,计算:(![]() )﹣1﹣3tan60°+
)﹣1﹣3tan60°+![]()
(3)利用(1)题中结论解答:如图2,直线l:y=![]() x与x轴所夹的锐角为α,直线l上点A的横坐标为1,求∠α.
x与x轴所夹的锐角为α,直线l上点A的横坐标为1,求∠α.