题目内容
 已知点A(5,0),点A关于直线y=kx(k>0)的对称点B正好落在反比例函数y=
已知点A(5,0),点A关于直线y=kx(k>0)的对称点B正好落在反比例函数y=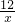 第一象限的图象,则k=________.
第一象限的图象,则k=________.
 或
或
分析:根据反比例函数图象上的点的坐标特征设B(a,
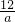 ),根据点的对称表示出AB的中点坐标,然后代入直线解析式整理表示出k,再根据对称性AB与直线互相垂直斜率之积等于-1列式表示出k,然后消掉k得到关于a的方程,求出a的值,再代入求出k的值即可.
),根据点的对称表示出AB的中点坐标,然后代入直线解析式整理表示出k,再根据对称性AB与直线互相垂直斜率之积等于-1列式表示出k,然后消掉k得到关于a的方程,求出a的值,再代入求出k的值即可.解答:设B(a,
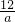 ),则
),则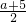 ,
, =
= ,
,所以,AB的中点坐标为(
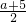 ,
, ),
),∴
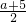 k=
k= ,
,∴k=
 ,
,∵A、B关于直线y=kx对称,
∴
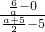 =-
=-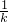 ,
,整理得,k=-
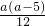 ,
,∴
 =-
=-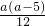 ,
,整理得,a4-25a2+144=0,
解得a2=16或a2=9,
∵反比例函数图象在第一象限,
∴a>0,
∴a=4或3,
当a=4时,k=
 =
= ,
,当a=3时,k=
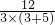 =
= ,
,综上所述,k的值为
 或
或 .
.故答案为:
 或
或 .
.点评:本题考查的是反比例函数图象上点的坐标特点,主要利用了点的对称与直线的互相垂直以及直线上点的坐标特征,利用两种方法表示出k是解题的关键,也是本题的难点.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=
14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=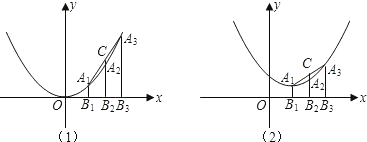 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.