题目内容
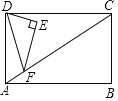
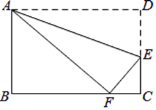
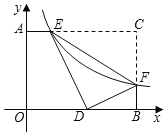
【题目】如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y![]() (k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为____.
(k>0)的图象与AC边交于点E,将△CEF沿E对折后,C点恰好落在OB上的点D处,则k的值为____.
【答案】![]() .
.
【解析】
先证明Rt△MED∽Rt△BDF,则 ,而EM:DB=ED:DF=4:3,求出DB,在Rt△DBF中,利用勾股定理即可求解.
,而EM:DB=ED:DF=4:3,求出DB,在Rt△DBF中,利用勾股定理即可求解.
如图,过点E作EM⊥x轴于点M,
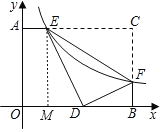
∵将△CEF沿EF对折后,C点恰好落在OB上的D点处,
∴∠EDF=∠C=90°,EC=ED,CF=DF,
∴∠MDE+∠FDB=90°,而EM⊥OB,
∴∠MDE+∠MED=90°,
∴∠MED=∠FDB,
∴Rt△MED∽Rt△BDF,
又∵EC=AC﹣AE=4![]() ,CF=BC﹣BF=3
,CF=BC﹣BF=3![]() ,
,
∴ED=4![]() ,DF=3
,DF=3![]() ,
,
∴ ,
,
∵EM:DB=ED:DF=4:3,而EM=3,
∴DB![]() ,
,
在Rt△DBF中,DF2=DB2+BF2,即(3![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得:k![]() ,
,
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息.
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价.
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A、B两类图书共1000本 2.A类图书不少于600本 | |
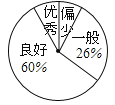
【题目】某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.