题目内容
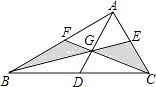
【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.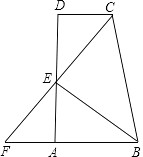
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
【答案】
(1)解:垂直,理由如下:
∵CD∥AB,
∴∠ABC+∠BCD=180°,
又∵∠ABC,∠BCD的角平分线交于E点,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∴∠EBC+∠ECB=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CEB=90°,
∴BE 与 CF 互相垂直.
(2)解:由(1)知∠CEB=90°,
∴∠FEB=90°,
在△FBE 和△CBE 中,
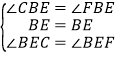
∴△FBE≌△CBE(ASA),
∴BF=BC,EF=EC,
又∵CD∥AB,
∴∠DCE=∠AFE,
在△DCE和△AFE中,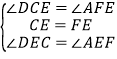
∴△DCE≌△AFE,
∴DC=AF,
∵CD=3,AB=4,
∴BC=BF=AF+AB=CD+AB=3+4=7,
【解析】(1)垂直,理由如下:由两直线平行,同旁内角互补得出∠ABC+∠BCD=180°;又由角平分线定义得出∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
从而得出∠EBC+∠ECB=90°,根据三角形内角和定理得出∠CEB=90°,即BE 与 CF 互相垂直.
(2)由(1)知∠CEB=∠FEB=90°,根据ASA得△FBE≌△CBE,再由全等三角形的性质得出BF=BC,EF=EC;又由两直线平行,内错角相等,得到∠DCE=∠AFE,由ASA得△DCE≌△AFE,再根据全等三角形的性质得出DC=AF,由已知条件和等量代换求出BC的值.
【考点精析】关于本题考查的角的平分线和平行线的性质,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案